题目描述
有一个未知的 $4\times4$ 的拼盘 $M$,它的每个元素都是正整数。给出 $4$ 行元素的总和 $4$ 列元素的总和以及两条对角线元素总和。另外还给出了拼盘中任意 $4$ 个位置的元素值,它们的位置在输入文件中给定
编写一个程序求出拼盘中另外 $12$ 个位置的正整数的值,要求这些元素的行之和,列之和以及对角线之和与输入文件中给定的值相一致
思路
首先题目给了我们每列每排和对角线的数的和,以及 $4$ 个数的数值,而且任何行对角线或列之和不会超过 $300$,另外给定的输入文件总是存在解决方案
假设题目给的数为 $sum_i$(从下标 $0$ 开始计数),下图一种颜色代表一个 $sum_i$ 的所管辖的数,也是约束情况合理的条件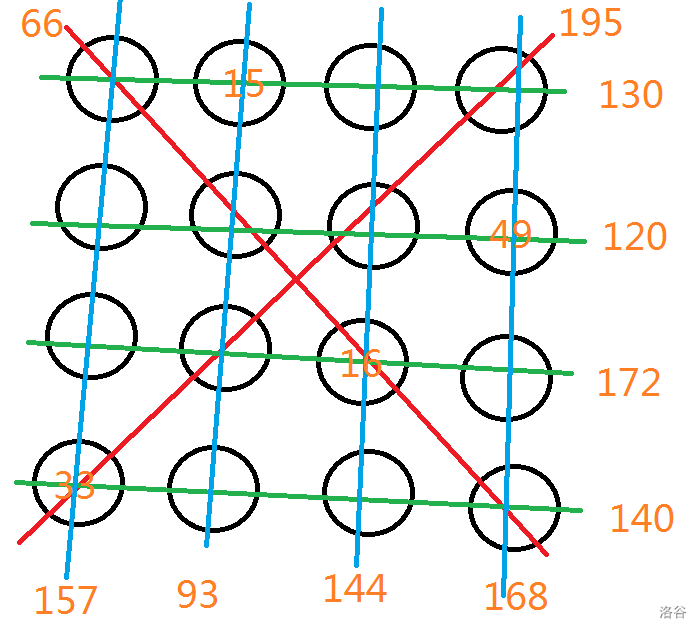
(样例)
目标:我们要找到更多的约束条件(因为约束越多,尝试的情况越少)
设 $S = sum_0+sum_1+sum_2+sum_3$(即所有数值和)
$\because$
$\therefore$ $\frac{(sum_0+sum_3+sum_5+sum_6+sum_8+sum_9)}{2}=S-(1,0)-(2,0)-(1,3)-(2,3)$
$S_1=(1,0)+(2,0)+(1,3)+(2,3)$(下图中紫色所经过的点的和)
$S_2=(0,1)+(0,2)+(3,1)+(3,2)=S-(sum_8+sum_9)-S_1$(下图中橙色所经过的点的和)
$S_3=(0,0)+(0,3)+(3,0)+(3,3)=(sum_0+sum_3)-S_2$(即四个角的和)
$S_4=S-S_1-S_2-S_3=(1,1)+(1,2)+(2,1)+(2,2)$(即内部四数之和)
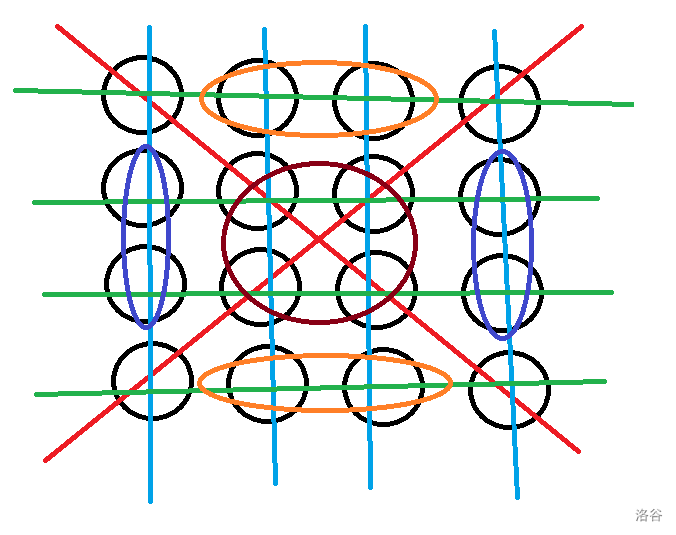
我们可以开始尝试一下了
我们先用样例的数据,为了方便我们用 $\times$ 表示已知数,$?$ 表示未知,$1$ 至 $n$ 表示我们自己填的数
初始:
$ ? , \times , ? , ? $
$ ? , ? , ? , \times $
$ ? , ? , \times , ? $
$ \times , ? , ? , ? $
填入第一个数
$ 1 , \times , ? , ? $
$ ? , ? , ? , \times $
$ ? , ? , \times , ? $
$ \times , ? , ? , ? $
填入第二个数
$ 1 , \times , 2 , \times $
$ ? , ? , ? , \times $
$ ? , ? , \times , ? $
$ \times , ? , ? , ? $
$ 1 , \times , 2 , \times $
$ ? , ? , ? , \times $
$ ? , ? , \times , ? $
$ \times , ? , ? , \times $(我们有 $S_3$)
$ 1 , \times , 2 , \times $
$ ? , \times , ? , \times $
$ ? , ? , \times , \times $
$ \times , ? , ? , \times $
填入第三个数
$ 1 ,\times, 2 , \times $
$ 3 , \times , \times , \times $
$ \times , \times , \times , \times $
$ \times , \times , \times , \times $
正是因为我们的约束条件找得多,所以我们需要填的数次数少,便利的次数就会减少(填的数只需要 $3$ 或 $4$ 个就可以得出答案!)
而剩下的就可以移交给随机数来处理了
通过 $sum_i$ 的范围限制,不断尝试即可。

