LCT动态树

题解 数据结构 线段树 平衡树 LCT
Markdown
发布日期:   2021-09-27
更新日期:   2021-12-23
文章字数:   2.6k
阅读次数:  

$LCT$

P3690 【模板】动态树（Link Cut Tree）

树

$LCT$ 可以理解为很多棵 $Splay$ 组合而成，但是由于每个节点只能有左右两个儿子，但很多点可以有共同的父亲，所以分为实边和虚边。

  • 实边：儿子和父亲互相可以到达，互相相认。
  • 虚边：儿子认爹，爹不认儿子。

原图

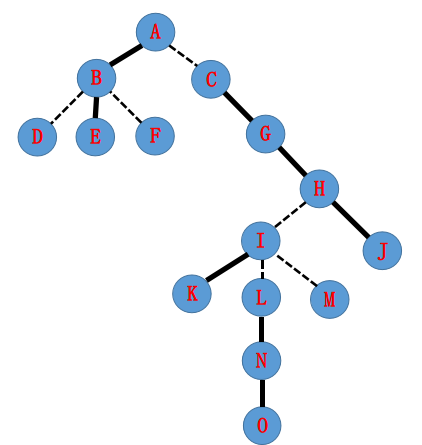
这就是一颗 $LCT$，$A$ 和 $B$ 互有联系是实边，而 $C$ 认 $A$ 为父亲，但是 $A$ 不认 $C$ 这个儿子，所以是虚边。

根据平衡树的性质，将所有平衡树旋转操作，尽量平衡。（注意换根后，连接的对象要变。）

平衡树划分

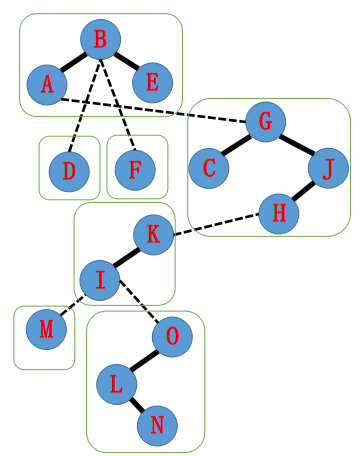
每一个绿框中都是一颗平衡树，注意除了最上面的平衡树，每棵平衡树的根都会和上面的平衡树连虚边。

路径异或和

将两个端点的路径全部变为实根，不断更新节点信息

目标状态

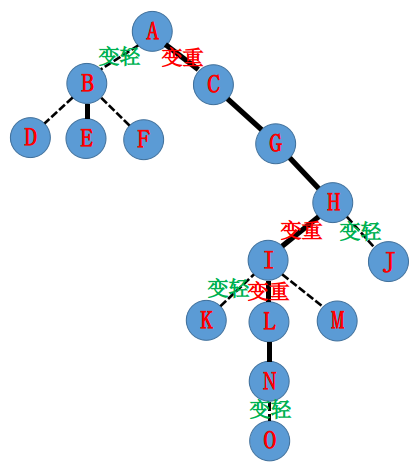
实虚边变换过程

原树：
原树

从目标处开始处理，实虚边转换。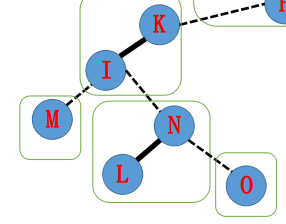
变换-1

继续处理。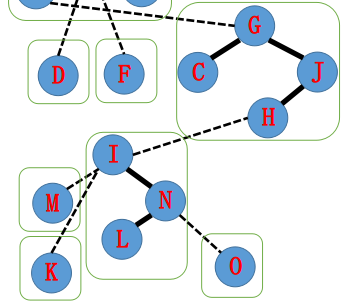
变换-2

向上处理。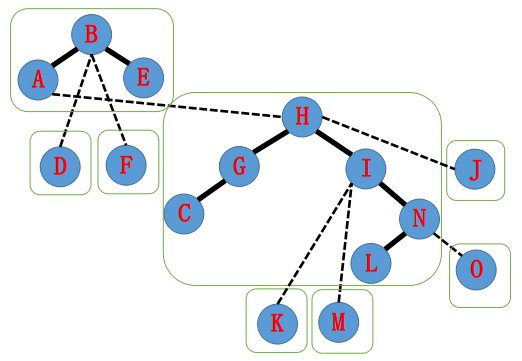
变换-3

处理到目标处结束。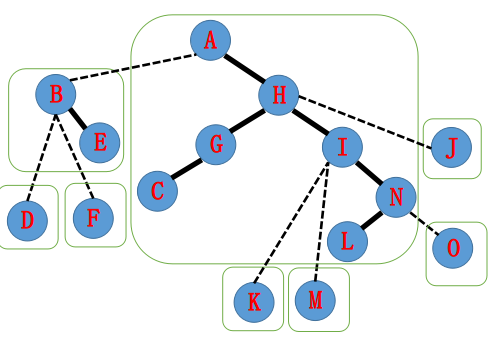
处理完成

即为目标的路径的相对平衡的树。
目标图
（图片来源自网络）

异或和

可以利用平衡树的性质，在旋转变换的同时维护节点信息，即异或和，完成变换后直接访问根节点异或和即为子树的异或和，而子树即为路径。

代码实现

大体思路：

  • 路径虚实边变换
  • 平衡树左右旋操作
  • 加边
  • 删边
  • 节点改值

变量名意义

int n,m;
int a_a[o_o];//原序列 
int s_n[o_o][2];//左右儿子 
int f_a[o_o];//父节点 
int s_z[o_o];//当前数的子树异或和 
int l_n[o_o];//懒标记（左右儿子翻转） 
int t_p;//路径长度（当前点到根节点） 
int l_j[o_o];//路径经过的节点（当前点到根节点）

节点初值

for(int i=1;i<=n;i++){
    	a_a[i]=r_r();//节点初值 
		s_z[i]=a_a[i];//初始化子树异或和 
	}

路径异或和

void u_p(int x){//更新节点信息（子树异或和） 
	s_z[x]=s_z[s_n[x][0]]^s_z[s_n[x][1]]^a_a[x];
}
void p_d(int x){//释放懒标记 
    int l=s_n[x][0],r=s_n[x][1];
    if(l_n[x]){//释放懒标记 
        l_n[l]^=1;//下传懒标记 
		l_n[r]^=1;
		l_n[x]=0;
        swap(s_n[x][0],s_n[x][1]);//交换左右子树 
    }
}
bool i_g(int x){//返回 1： 不是实边（虚边，不是同一个平衡树），否则是实边 
	return s_n[f_a[x]][0]!=x&&s_n[f_a[x]][1]!=x;
}
void l_r(int x){//旋转 
    int y=f_a[x],z=f_a[y],l,r;
    if(s_n[y][0]==x)l=0;//当前节点是父节点左儿子 
	else l=1;//当前节点是父节点右儿子 
	r=l^1;//另一个儿子 
    if(!i_g(y)){//父节点在树上 
		if(s_n[z][0]==y)s_n[z][0]=x;//父节点在爷节点的左节点，更新为当前节点 
		else s_n[z][1]=x;//爷节点的右儿子更新为当前节点 
	}
    f_a[x]=z;//更新 x 的父节点 
	f_a[y]=x;//更新 y 的父节点 
	f_a[s_n[x][r]]=y;//更新 x 的另一个节点的父亲（没改变的节点的父亲的值仍是当前节点，要更新）  
    s_n[y][l]=s_n[x][r];//未更新节点接到父节点的转动的子树上 
	s_n[x][r]=y;//转动的子树变为父节点 
    u_p(y);//更新新子节点 
	u_p(x);//更新新当前节点 
}
void p_h(int x){//平衡树维护 
    t_p=1;//初始化路径长度（当前点到根节点） 
	l_j[t_p]=x;//记录当前节点 
    for(int i=x;!i_g(i);i=f_a[i])l_j[++t_p]=f_a[i];//记录到根一路上的节点 
    for(int i=t_p;i;i--)p_d(l_j[i]);//释放懒标记 
    while(!i_g(x)){//在同一棵平衡树上 
        int y=f_a[x],z=f_a[y];//记录父节点和爷节点 
        if(!i_g(y)){//父节点在树上 
            if((s_n[y][0]==x)^(s_n[z][0]==y))l_r(x);//有“折点”，以 x 旋 
            else l_r(y);//以 y 旋（尽量平衡） 
        }
		l_r(x);//以 x 旋 
    }
}
void r_d(int x){//将 x 遍历到总根路径上虚实边变换 
	for(int t=0;x;t=x,x=f_a[x]){//将 x 翻转到总根（遍历虚边，跨树向上爬） 
		p_h(x);//将 x 上转到当前跟 
		s_n[x][1]=t;//更新右子节点 
		u_p(x);//更新节点信息 
	}
}
void n_g(int x){//连通路径 
	r_d(x);//将 x 遍历到总根 
	p_h(x);//平衡树换根（x 遍历到当前平衡树的根） 
	l_n[x]^=1;//打懒标记 
}
int f_i(int x){//x 所在树的根 
	r_d(x);//将 x 遍历到总根 
	p_h(x);//平衡树换根（x 遍历到当前平衡树的根） 
	while(s_n[x][0])x=s_n[x][0];
	return x;
}
void n_t(int x,int y){//x 到 y 之间路径建新树，以 y 为根 
	n_g(x);//连通路径 
	r_d(y);//将 y 遍历到总根 
	p_h(y);//平衡树换根（y 遍历到当前平衡树的根） 
}
int main(){
	....
	if(op==0){
            int x=r_r(),y=r_r();
			n_t(x,y);//建 x 到 y 链之间的新树 
            printf("%d\n",s_z[y]);//输出结果（y 为根）树即为范围 
        }
	....
}

加边

void a_d(int x,int y){//x，y 连一条边  
	n_g(x);//换根 
	f_a[x]=y;//x 的父节点为 y（虚根） 
}
int main(){
	....
	if(op==1){
            int x=r_r(),y=r_r(),f_x=f_i(x),f_y=f_i(y);
            if(f_x!=f_y)a_d(x,y);//不在一个平衡树加边，否则会形成环 
        }
	....
}

删边

void d_l(int x,int y){//删边 
	n_t(x,y);//建新树 
	if(s_n[y][0]==x&&s_n[x][1]==0){//x 不是左儿子并且 x 没有右儿子 
		s_n[y][0]=0;//断左子节点 
		f_a[x]=0;//断父节点 
	} 
}
int main(){
	....
	if(op==2){
            int x=r_r(),y=r_r(),f_x=f_i(x),f_y=f_i(y);
            if(f_x==f_y)d_l(x,y);//在同一个树中，删边 
        }
	....
}

改权值

if(op==3){
        int x=r_r(),y=r_r();
        r_d(x);//将 x 遍历到总根
		p_h(x);//平衡树换根（x 遍历到当前平衡树的根） 
		a_a[x]=y;//更新新值 
		u_p(x);//更新节点信息 
}

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<cctype>
#include<queue>
using namespace std;
long long r_r(){//快读 
	long long k=0,f=1;
	char c=getchar();
	while(!isdigit(c)){
		if(c=='-')f=-1;
		c=getchar();
	}
	while(isdigit(c)){
		k=(k<<1)+(k<<3)+(c^48);
		c=getchar(); 
	}
	return k*f;
}
const int o_o=1e6+10;//数组下标 
int n,m;
int a_a[o_o];//原序列 
int s_n[o_o][2];//左右儿子 
int f_a[o_o];//父节点 
int s_z[o_o];//当前数的子树异或和 
int l_n[o_o];//懒标记（左右儿子翻转） 
int t_p;//路径长度（当前点到根节点） 
int l_j[o_o];//路径经过的节点（当前点到根节点）
void u_p(int x){//更新节点信息（子树异或和） 
	s_z[x]=s_z[s_n[x][0]]^s_z[s_n[x][1]]^a_a[x];
}
void p_d(int x){//释放懒标记 
    int l=s_n[x][0],r=s_n[x][1];
    if(l_n[x]){//释放懒标记 
        l_n[l]^=1;//下传懒标记 
		l_n[r]^=1;
		l_n[x]=0;
        swap(s_n[x][0],s_n[x][1]);//交换左右子树 
    }
}
bool i_g(int x){//返回 1： 不是实边（虚边，不是同一个平衡树），否则是实边 
	return s_n[f_a[x]][0]!=x&&s_n[f_a[x]][1]!=x;
}
void l_r(int x){//旋转 
    int y=f_a[x],z=f_a[y],l,r;
    if(s_n[y][0]==x)l=0;//当前节点是父节点左儿子 
	else l=1;//当前节点是父节点右儿子 
	r=l^1;//另一个儿子 
    if(!i_g(y)){//父节点在树上 
		if(s_n[z][0]==y)s_n[z][0]=x;//父节点在爷节点的左节点，更新为当前节点 
		else s_n[z][1]=x;//爷节点的右儿子更新为当前节点 
	}
    f_a[x]=z;//更新 x 的父节点 
	f_a[y]=x;//更新 y 的父节点 
	f_a[s_n[x][r]]=y;//更新 x 的另一个节点的父亲（没改变的节点的父亲的值仍是当前节点，要更新）  
    s_n[y][l]=s_n[x][r];//未更新节点接到父节点的转动的子树上 
	s_n[x][r]=y;//转动的子树变为父节点 
    u_p(y);//更新新子节点 
	u_p(x);//更新新当前节点 
}
void p_h(int x){//平衡树维护 
    t_p=1;//初始化路径长度（当前点到根节点） 
	l_j[t_p]=x;//记录当前节点 
    for(int i=x;!i_g(i);i=f_a[i])l_j[++t_p]=f_a[i];//记录到根一路上的节点 
    for(int i=t_p;i;i--)p_d(l_j[i]);//释放懒标记 
    while(!i_g(x)){//在同一棵平衡树上 
        int y=f_a[x],z=f_a[y];//记录父节点和爷节点 
        if(!i_g(y)){//父节点在树上 
            if((s_n[y][0]==x)^(s_n[z][0]==y))l_r(x);//有“折点”，以 x 旋 
            else l_r(y);//以 y 旋（尽量平衡） 
        }
		l_r(x);//以 x 旋 
    }
}
void r_d(int x){//将 x 遍历到总根路径上虚实边变换 
	for(int t=0;x;t=x,x=f_a[x]){//将 x 翻转到总根（遍历虚边，跨树向上爬） 
		p_h(x);//将 x 上转到当前跟 
		s_n[x][1]=t;//更新右子节点 
		u_p(x);//更新节点信息 
	}
}
void n_g(int x){//连通路径 
	r_d(x);//将 x 遍历到总根 
	p_h(x);//平衡树换根（x 遍历到当前平衡树的根） 
	l_n[x]^=1;//打懒标记 
}
int f_i(int x){//x 所在树的根 
	r_d(x);//将 x 遍历到总根 
	p_h(x);//平衡树换根（x 遍历到当前平衡树的根） 
	while(s_n[x][0])x=s_n[x][0];
	return x;
}
void n_t(int x,int y){//x 到 y 之间路径建新树，以 y 为根 
	n_g(x);//连通路径 
	r_d(y);//将 y 遍历到总根 
	p_h(y);//平衡树换根（y 遍历到当前平衡树的根） 
}
void d_l(int x,int y){//删边 
	n_t(x,y);//建新树 
	if(s_n[y][0]==x&&s_n[x][1]==0){//x 不是左儿子并且 x 没有右儿子 
		s_n[y][0]=0;//断左子节点 
		f_a[x]=0;//断父节点 
	} 
}
void a_d(int x,int y){//x，y 连一条边  
	n_g(x);//换根 
	f_a[x]=y;//x 的父节点为 y（虚根） 
}
int main(){
    n=r_r();m=r_r();
    for(int i=1;i<=n;i++){
    	a_a[i]=r_r();//节点初值 
		s_z[i]=a_a[i];//初始化子树异或和 
	}
    while(m--){
        int op=r_r();
        if(op==0){
            int x=r_r(),y=r_r();
			n_t(x,y);//建 x 到 y 链之间的新树 
            printf("%d\n",s_z[y]);//输出结果（y 为根）树即为范围 
        }else if(op==1){
            int x=r_r(),y=r_r(),f_x=f_i(x),f_y=f_i(y);
            if(f_x!=f_y)a_d(x,y);//不在一个平衡树加边，否则会形成环 
        }else if(op==2){
            int x=r_r(),y=r_r(),f_x=f_i(x),f_y=f_i(y);
            if(f_x==f_y)d_l(x,y);//在同一个树中，删边 
        }else {
            int x=r_r(),y=r_r();
            r_d(x);//将 x 遍历到总根
			p_h(x);//平衡树换根（x 遍历到当前平衡树的根） 
			a_a[x]=y;//更新新值 
			u_p(x);//更新节点信息 
        }
    }
    return 0;
}
文章作者: 王大神——A001
文章链接: http://wdsa001.github.io/2021/09/27/lct-dong-tai-shu/
版权声明: 本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 王大神——A001 !
题解 数据结构 线段树 平衡树 LCT
  目录