扫描线
现在我们有一些矩形在平面直角坐标系上:
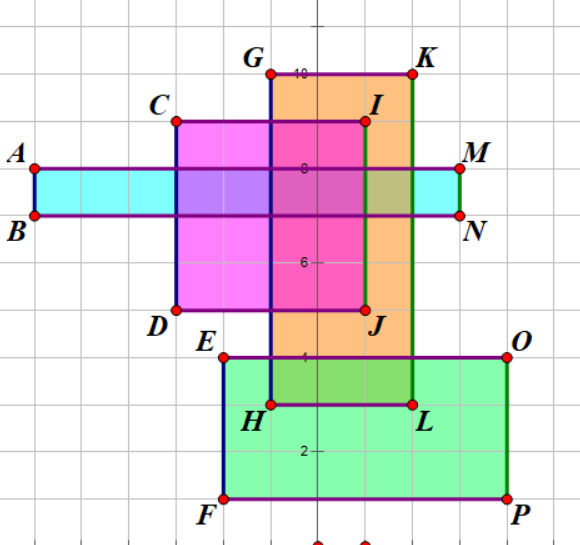
现在我们要求他们的面积的并(平面直角坐标系被覆盖的面积)
我们可以将每个矩形看成有两条线组成(左边一条为蓝色,右边一条为绿色)
将所有的蓝色线标记成 $+1$,将所有的绿色线标记为 $-1$ ,从左向右扫得到的数值即为当前点被覆盖的次数,又与我们求的是并,所以只记录有无被覆盖过即可(记录被覆盖几次是记录所有矩形的面积)。
将所有线段处理出来后可以用线段树维护,每次维护的是整个 $y$ 轴($1$ 维直线)每次统计两次之间的 $x$ 的差和之间 $y$ 轴上的长度相乘即可。
扫描的过程
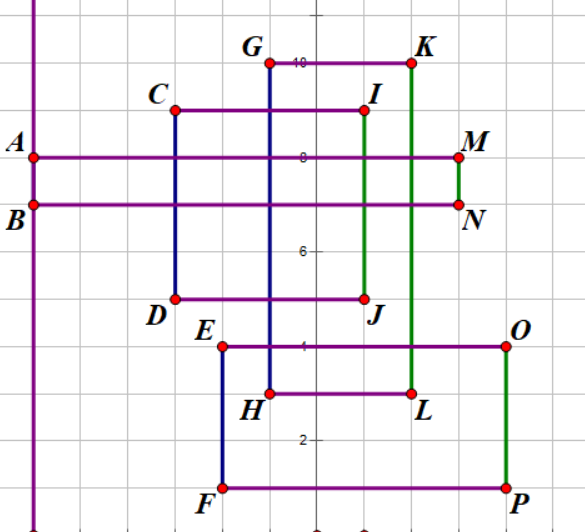
记录 $A,B$ 坐标,$y_{[B,A]}$ 更新到线段树上。
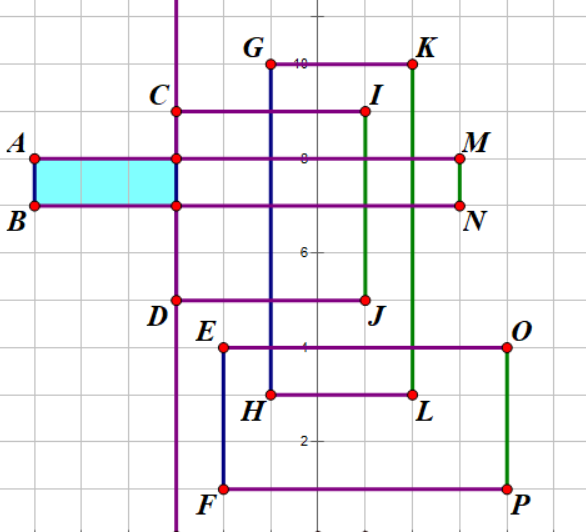
统计记录 $(y_A-y_B)\times (x_C-x_A)$(小矩形面积)
记录 $C,D$ 坐标,$y_{[D,C]}$ 更新到线段树上。
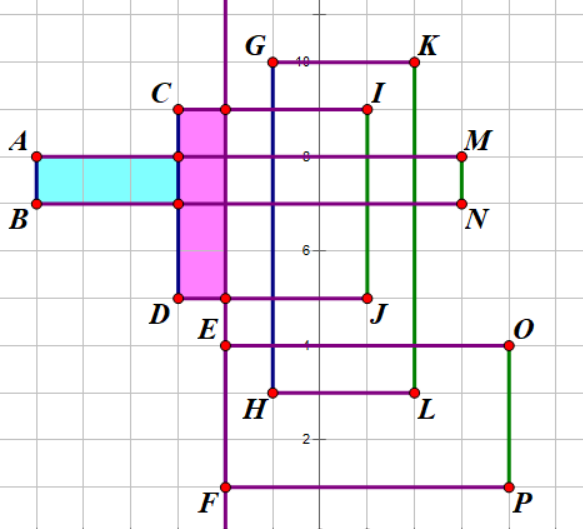
统计记录 $(y_C-y_D)\times (x_E-x_D)$(小矩形面积)
记录 $E,F$ 坐标,$y_{[F,E]}$ 更新到线段树上。
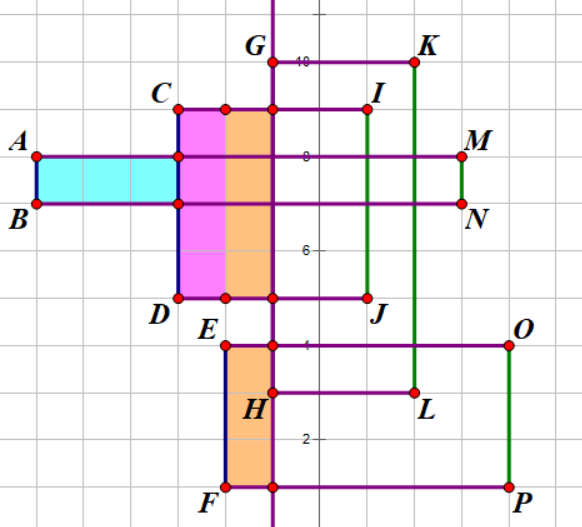
统计记录 $((y_C-y_D)+(y_E-y_F))\times (x_H-x_F)$(小矩形面积)
记录 $G,H$ 坐标,$y_{[H,G]}$ 更新到线段树上。
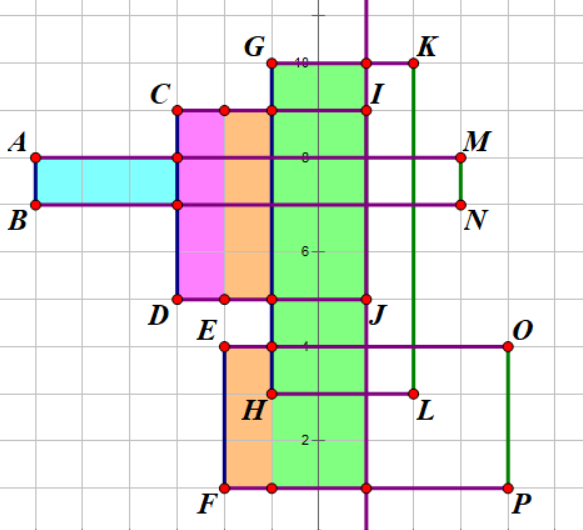
统计记录 $(y_G-y_F)\times (x_I-x_G)$(小矩形面积)
记录 $I,J$ 坐标,$y_{[J,I]}$ 更新到线段树上(值为负,说明有矩形到头了,要更新回去)。
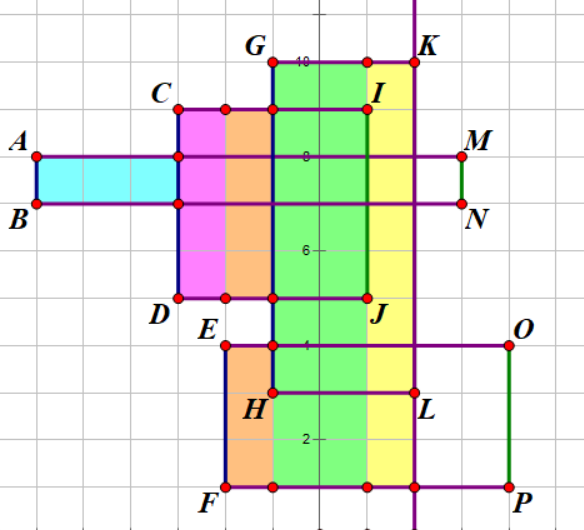
统计记录 $(y_G-y_F)\times (x_K-x_I)$(小矩形面积)
记录 $K,L$ 坐标,$y_{[L,K]}$ 更新到线段树上。
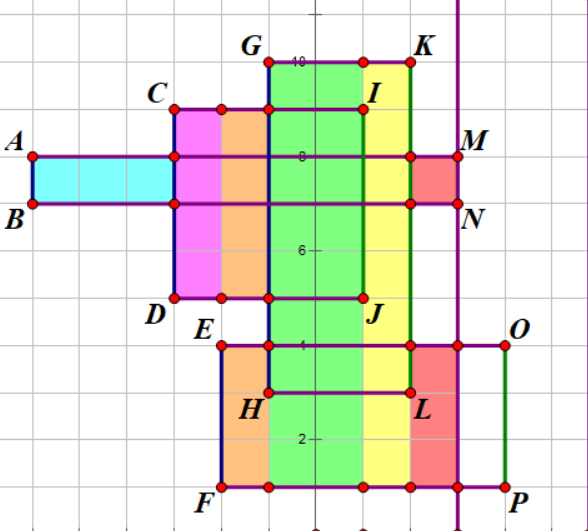
统计记录 $((y_B-y_A)+(y_E-y_F))\times (x_M-x_K)$(小矩形面积)
记录 $M,N$ 坐标,$y_{[N,M]}$ 更新到线段树上。
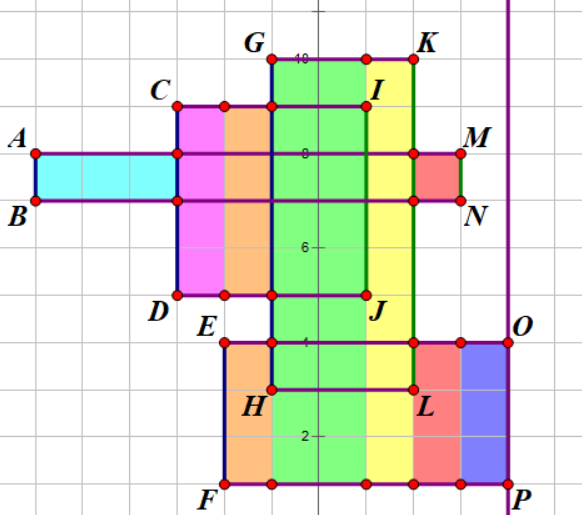
统计记录 $(y_E-y_F)\times (x_O-x_M)$(小矩形面积)
记录 $O.P$ 坐标,$y_{[P,O]}$ 更新到线段树上。
代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<string>
#include<cmath>
using namespace std;
int r_r(){//快读
int k=0,f=1;
char c=getchar();
while(!isdigit(c)){
if(c=='-')f=-1;
c=getchar();
}
while(isdigit(c)){
k=(k<<1)+(k<<3)+(c^48);
c=getchar();
}
return k*f;
}
const int o_o=1e6+10;
struct po{
long long l,r;//记录线段在 y 轴的左右边界
long long x;//记录 x 的坐标
long long v;//记录位置(左边界右边界)
bool operator<(po b){//x 坐标从小到大排序,x长度相同,长度长的优先
return x==b.x?l>b.l:x<b.x;
}
}l[o_o];
struct pp{
int s_m;//节点价值
int l_n;//长度
pp(){
s_m=l_n=0;//初始化
}
}t_r[o_o<<2];
long long n,t_t=0,a_s=0,y_y[o_o];
void u_p(int k,int l,int r){
if(t_r[k].s_m>0)t_r[k].l_n=y_y[r]-y_y[l];//这一段被覆盖,更新长度
else t_r[k].l_n=t_r[k<<1].l_n+t_r[k<<1|1].l_n;//更新长度
}
void a_d(int k,int l,int r,int x,int y,int v){
if(x>=y_y[r]||y_y[l]>=y) return;//没有重合部分
if(x<=y_y[l]&&y_y[r]<=y){
t_r[k].s_m+=v;//更新值
u_p(k,l,r);
return ;
}
int m_i=(l+r)>>1;
a_d(k<<1,l,m_i,x,y,v);//统计左边
a_d(k<<1|1,m_i,r,x,y,v);//统计右边
u_p(k,l,r);
}
int main(){
n=r_r();
for(int i=1,x_1,y_1,x_2,y_2;i<=n;i++){
x_1=r_r(),y_1=r_r(),x_2=r_r(),y_2=r_r();
//存入矩形基本信息
l[(i<<1)-1].x=x_1;
l[(i<<1)-1].l=y_1;
l[(i<<1)-1].r=y_2;
l[(i<<1)-1].v=1;//左边界标记
l[i<<1].x=x_2;
l[i<<1].l=y_1;
l[i<<1].r=y_2;
l[i<<1].v=-1;//右边界标记
//记录线段长度
y_y[(i<<1)-1]=y_1;
y_y[i<<1]=y_2;
}
n<<=1;
sort(y_y+1,y_y+n+1);//将所有的 y 坐标排序
sort(l+1,l+n+1);//将所有线段排序
for(int i=1;i<=n;i++)if(y_y[i]!=y_y[i+1])y_y[++t_t]=y_y[i];//去重
for(int i=1;i<n;i++){
a_d(1,1,n,l[i].l,l[i].r,l[i].v);//线段的值增加
a_s+=(l[i+1].x-l[i].x)*t_r[1].l_n;//统计结果
}
printf("%lld\n",a_s);
return 0;
}
