$S-T$ 割
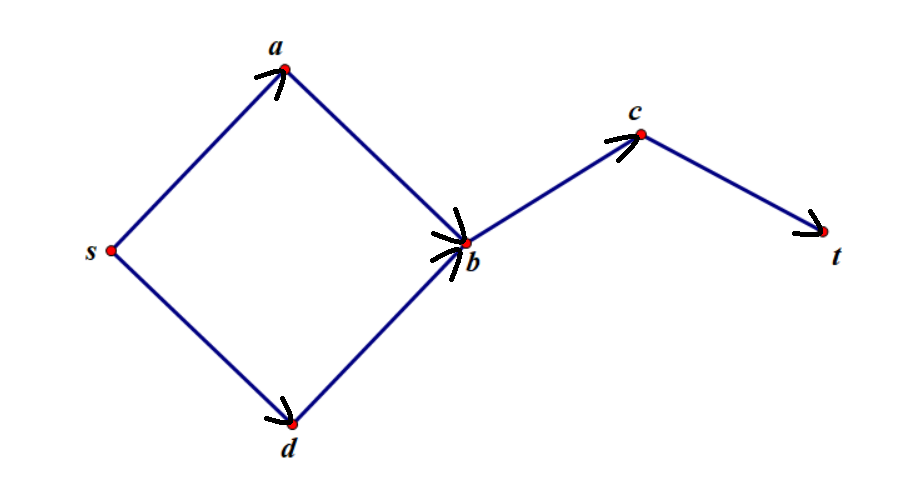
我们知道,判断从 $s$ 到 $t$ 是否存在路径,可以通过 $dfs$ 和 $bfs$ 判断即可,但是如何证明 $s\rightarrow t$ 存在路径呢?
为了方便理解,我们先将原图更改一下:
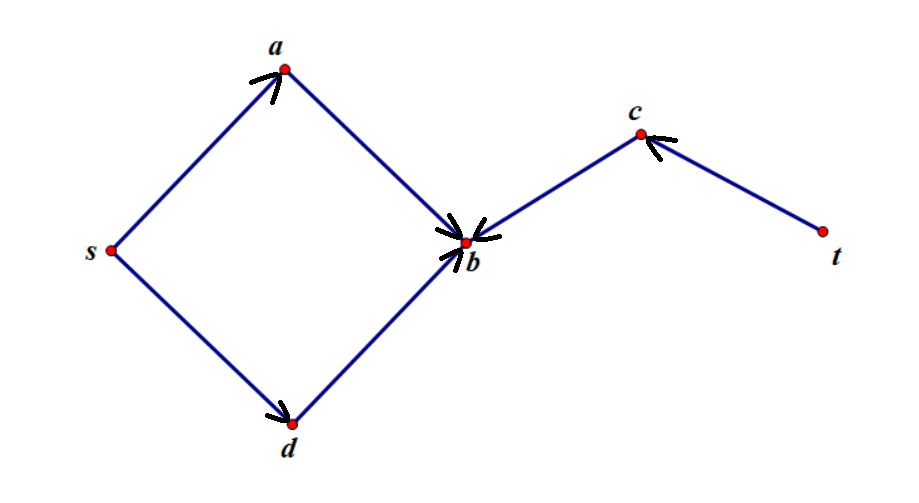
首先,我们通过一些“笨”方法来描述,先枚举所有 $s\rightarrow t$ 的可能路径,例如: $s\rightarrow t$,$s\rightarrow a\rightarrow t$,$s\rightarrow a\rightarrow b\rightarrow t$,$…$
一条 $s\rightarrow t$ 的路径一定在上面的列表中,但是找不到合法路径,所以不存在 $s\rightarrow t$ 的路径。
这么证明非常麻烦,我们不仅要枚举所有路径,还要判断其是否合法。
现在我们将整个图分成两部分:
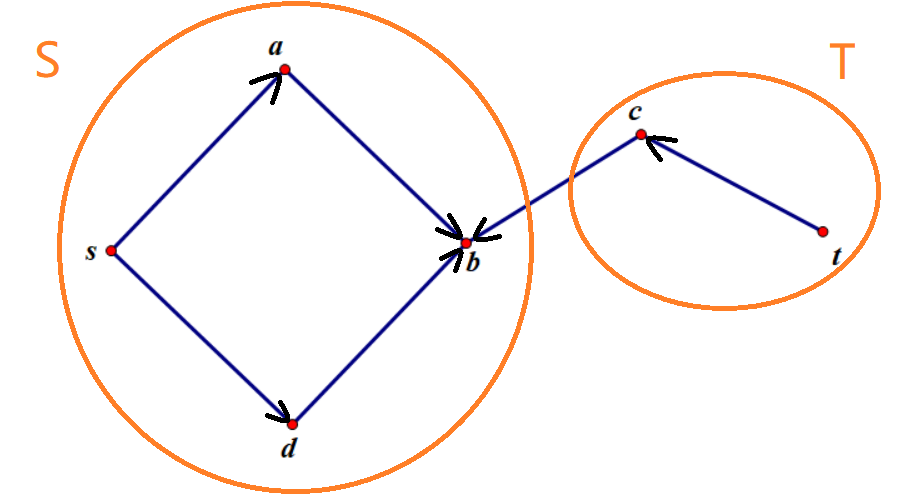
$S-T$ 割:割的大小为 $S\rightarrow T$ 中点连边的个数($S\rightarrow T$)
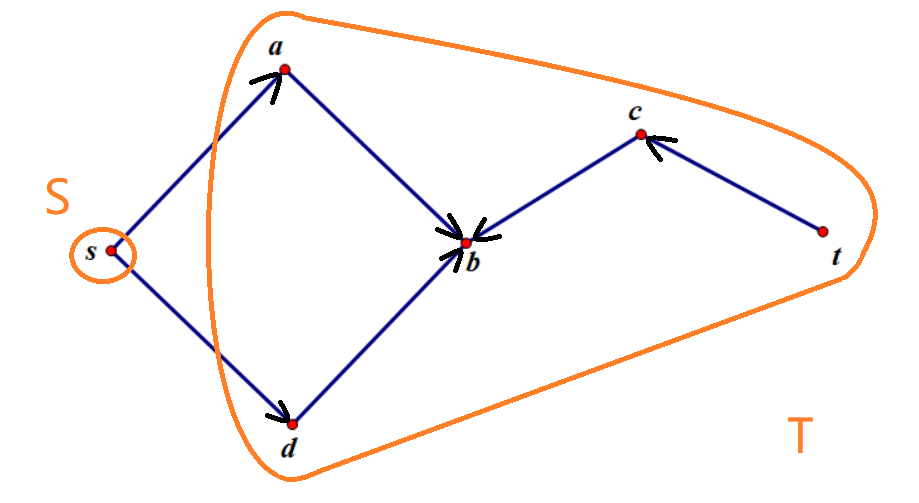
$S=\lbrace s\rbrace $
$T=\lbrace a,b,c,d,t\rbrace $
这种分割方法 $S\rightarrow T$ 有两条边,所以割边为 $2$。
集合分的点是在随意的,如下:
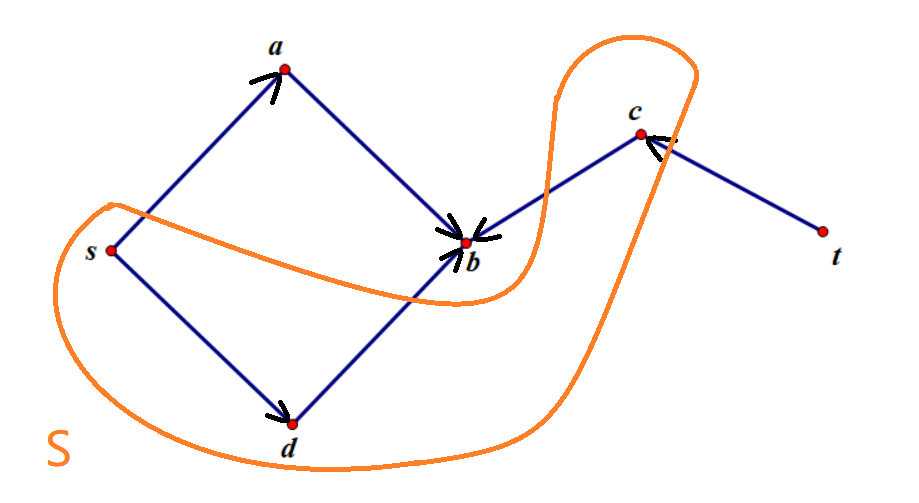
$S=\lbrace s,d,c\rbrace$
$T=\lbrace a,b,t\rbrace$
$S\rightarrow T$ 割边为 $3$。
大小为 $0$ 的 $S-T$ 割是“找不到路径”的证明。
求 $G$ 中最多有多少条不相交的 $S\rightarrow T$ 路径。
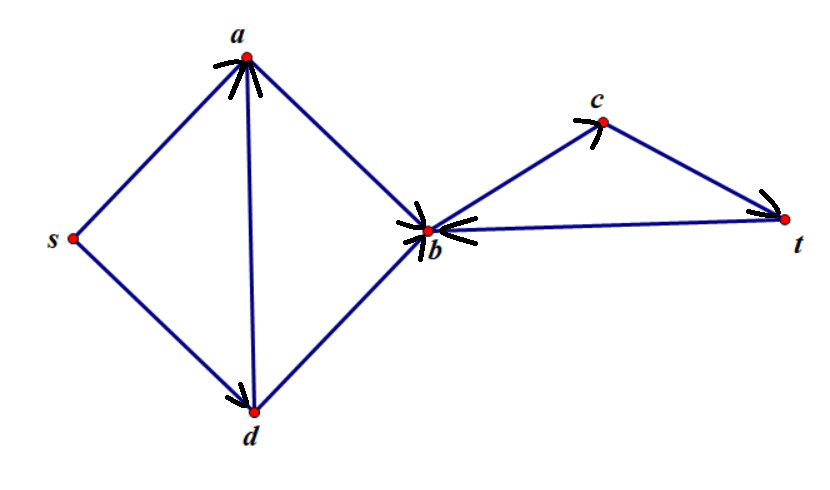
设不相交数量 $=k$
若 $k=1$,存在,那么可以找 $k=2$ 是否存在 $…$ 知道不存在为止。
我们先用一个相对简单的图学习一下。
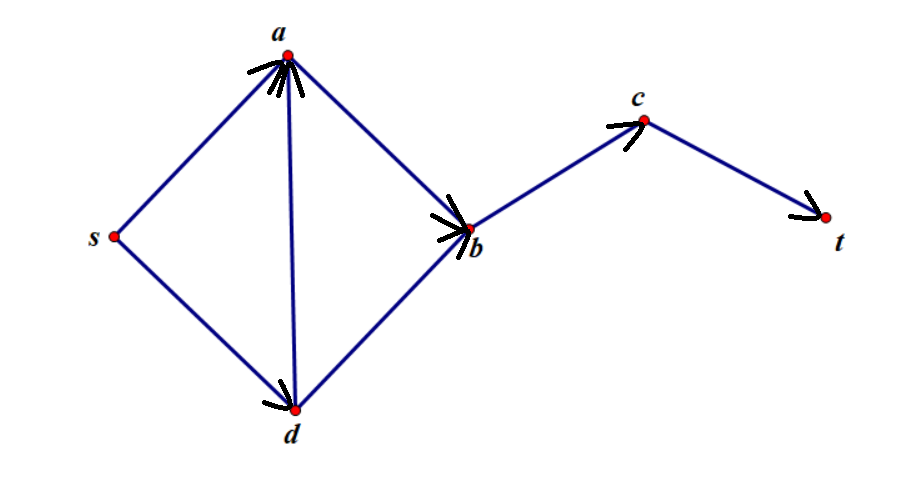
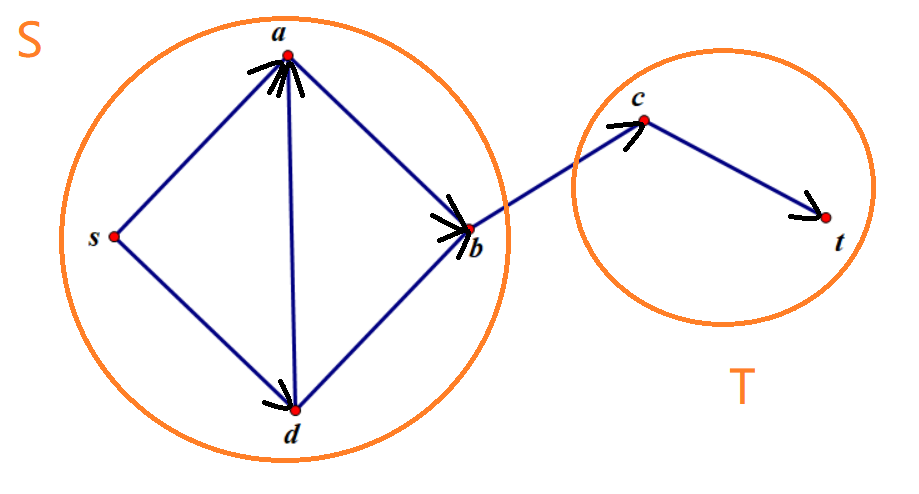
分成两个集合:$S=\lbrace a,b,c,s\rbrace,T=\lbrace c,t\rbrace$
枚举路径:
$s\rightarrow a\rightarrow b\rightarrow c\rightarrow t$
$s\rightarrow d\rightarrow b\rightarrow c\rightarrow t$
$s\rightarrow d\rightarrow a\rightarrow b\rightarrow c\rightarrow t$
如果发现 $S-T=1$,那么 $s,t$ 最多有一条路径($k\leqslant 1$),此时 $k=0$ 也是可能的。
不难发现:

所有的 $S-T$ 割都 $\geqslant 2$。
那么我们这么找路径呢?
我们可以随意找一条路径,然后不断“纠错”,统计答案个数(类似于求最长上升子序列的思路)
我们不幸的找到了路:$s\rightarrow d\rightarrow a\rightarrow b\rightarrow c\rightarrow t$
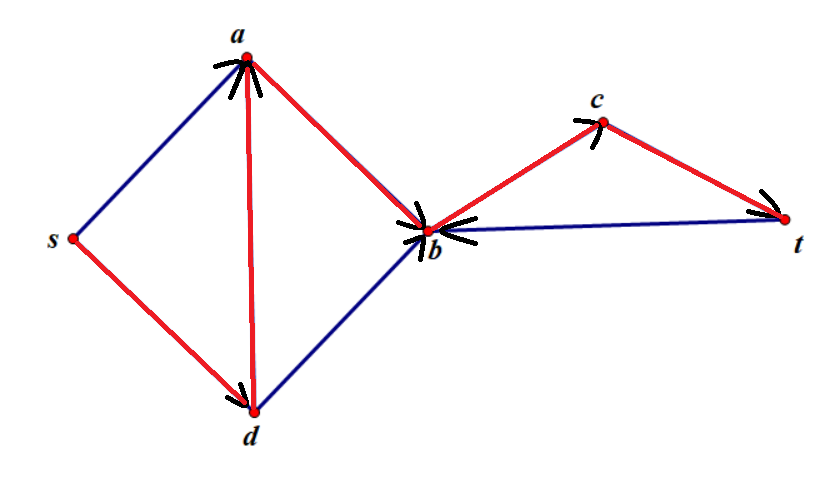
我们找到这条路后将所有经过的路径反转:
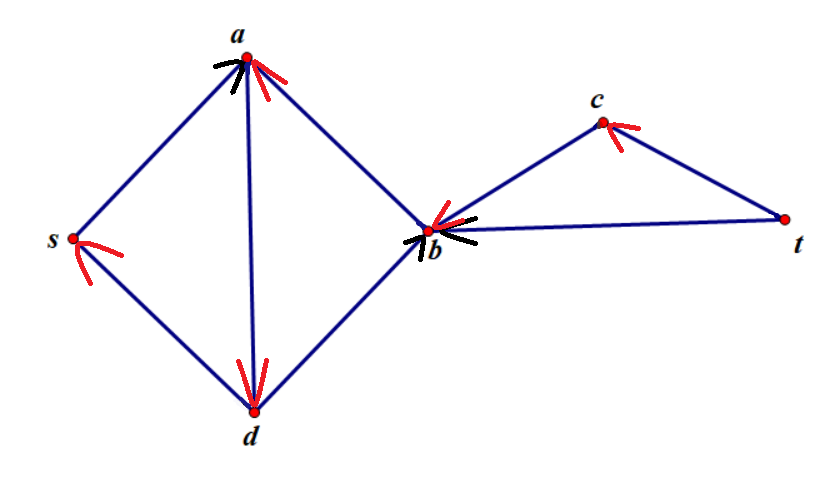
然后,我们继续找路:
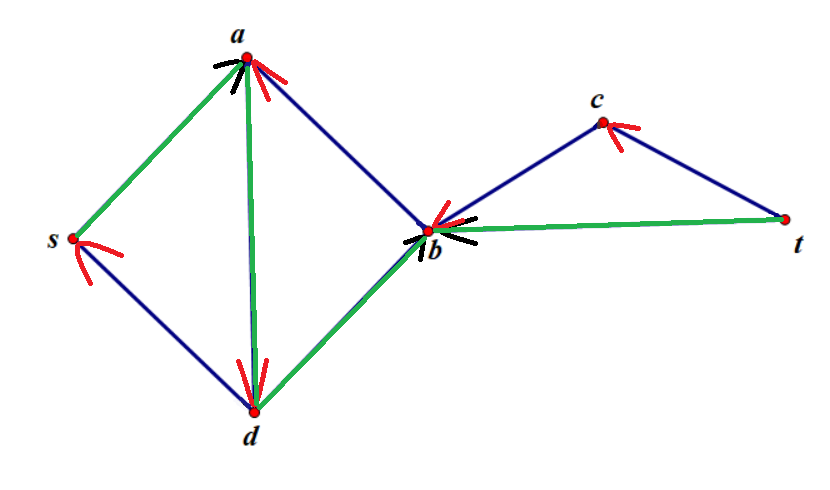
继续反转:
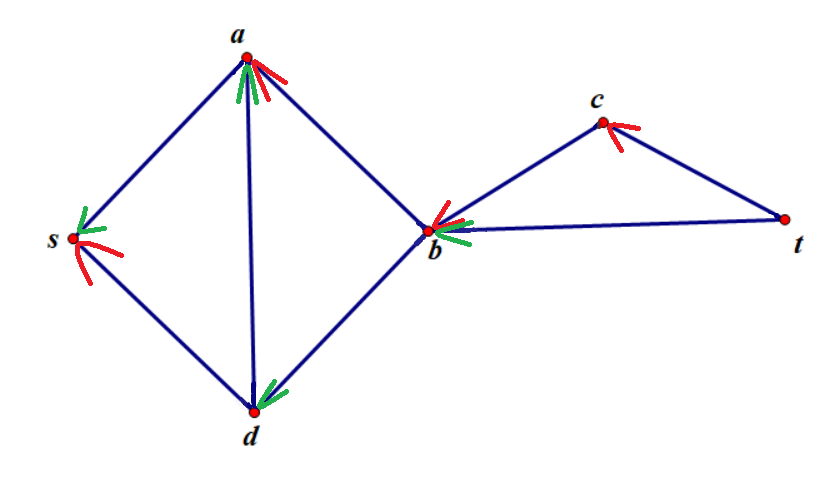
此时已经没有路径可以使 $S\rightarrow T$,所以结果为 $2$,而将路径反转的操作就是“纠错”。也叫作:$Ford-Fulkerson$ 残留网络。
残留网络
正确性证明:
站如现在已经找到了:$p1,p2,p3$这几条路径:
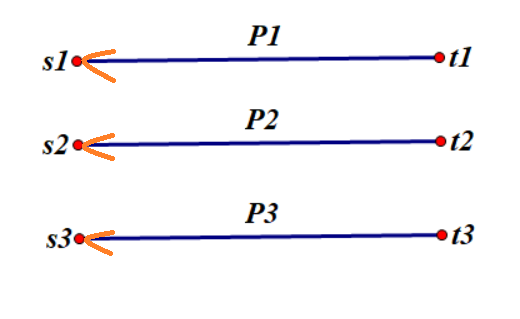
现在又发现了路径 $p4$ 的存在,那么我们要对原图进行一些修改:
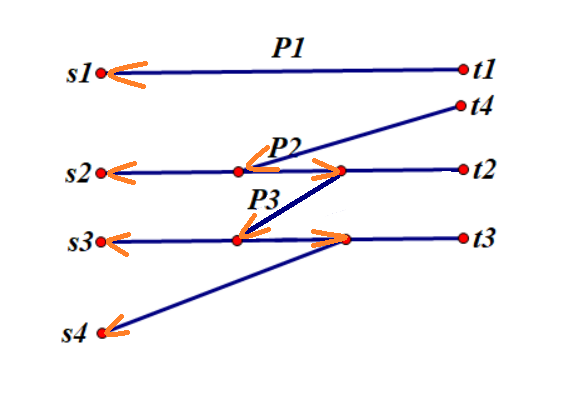
由于反转操作,中间重合的部分会断掉(因为新出现的 $p4$ 经过了这些道路,所以要“纠错”)
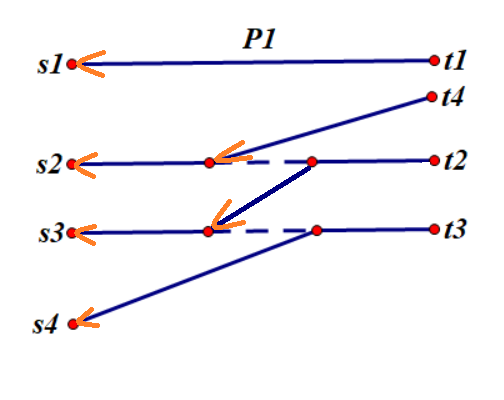
将编号图进行美化:
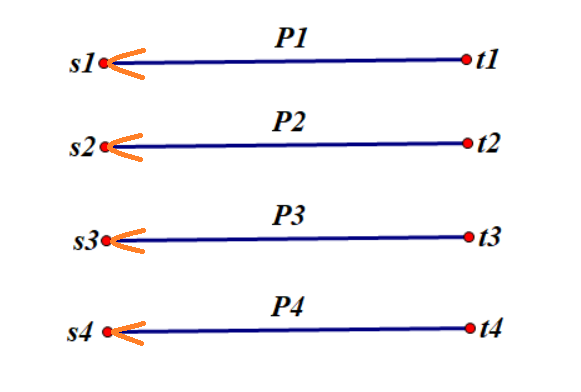
所以正确性没问题。
带权图(网络流)
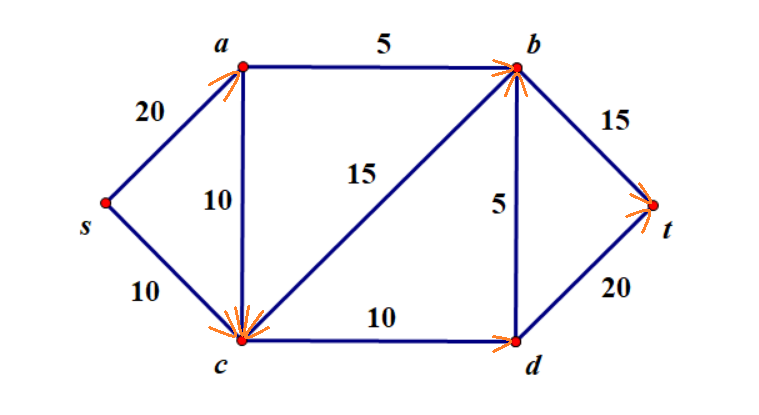
可以将每个边的权值看成很多个重边,例如:将 $s\rightarrow a$ 可以看成有 $20$ 个 $s\rightarrow a$ 边,然后不断进行“纠错”。
容量:$C_u,v$
流量:$x_i$
设
$x_1=s\rightarrow a\rightarrow b\rightarrow t$
$x_2=s\rightarrow a\rightarrow c\rightarrow d\rightarrow t$
$…$
$s\rightarrow a:x_1+x_2+…\leqslant 20$
$c\rightarrow d:x_2+x_3+…\leqslant 10$
$x_i\geqslant 0(1\leqslant i\leqslant p)$
这即是网络流的“原始”表达(线性规划)
设 $f(s,a)$ 表示为 $s\leftrightarrow a$ 边流量。
线性规划:
$f(s,a)=f(a,b)+f(a,c)$ (流出量守恒)
$f(a,b)=f(b,c)+f(b,t)$
$…$
可以想象成路径叠加。
线性规划“对偶”理论
最大值约束($\leqslant$)$\Leftrightarrow$ 最小值约束($\geqslant$)
最少的边能覆盖路径不就是 $S-T$ 割么!

