Dinic（最大流）

最大流

复习 网络流入门 反向弧（残留网络中改变路径流向的方式）知识。

最大流就是从源点最多能流向汇点的量。也是图论基础题。

首先正常一点的思路就是：建边，从源点开始尝试找路径，找到就记录，更新每条边的流量上限，不断找，直到不能流为止。

但是这样会导致有些路径并不是最优路径，所以就加上反向弧的优化，这样保证了最后计算的一定是最优解。

虽然结果却是无误，但是这样并不能通过本题，会发现有 $3$~$4$ 个点 TLE 。

P3376 【模板】网络最大流

普通代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<string>
#include<cctype>
using namespace std;
long long r_r(){
	long long x=0,f=1;
	char c=getchar();
	while(!isdigit(c)){
		if(c=='-')f=-1;
		c=getchar();
	}
	while(isdigit(c)){
		x=(x<<1)+(x<<3)+(c^48);
		c=getchar();
	}
	return x*f;
}
const int o_o=1e6+10;
int n=r_r(),m=r_r(),s=r_r(),t=r_r();
struct po{
	int n_t;
	int v;
	long long l;
}p_p[o_o];
int h_d[o_o],x_p=1;
void a_d(int u,int v,long long l){//建边
	p_p[++x_p].v=v;
	p_p[x_p].l=l;
	p_p[x_p].n_t=h_d[u];
	h_d[u]=x_p;
}
bool b_b[o_o];
long long f_i(int k,long long v_v){
	if(k==t)return v_v;//到目标点，输出 
	b_b[k]=1;//标记 
	for(int i=h_d[k];i;i=p_p[i].n_t){//枚举出边 
		int v=p_p[i].v;
		if(b_b[v]||!p_p[i].l)continue;//已经走过或者没有流量结束 
		int a_s=0;//统计结果 
		if(a_s=f_i(v,min(v_v,p_p[i].l))>0){//成功流向汇点 
			p_p[i].l-=a_s;//更新流出量 
			p_p[i^1].l+=a_s;//反向边更新流量 
			return a_s;
		}
	}
	return 0;
} 
int main(){
	for(int i=1;i<=m;i++){
		long long a=r_r(),b=r_r(),v=r_r();
		a_d(a,b,v);//连正向边 
		a_d(b,a,0);//建反向边 
	}
	long long a_s=0,s_m=0;//初始化答案 
	while(1){
		memset(b_b,0,sizeof b_b);//更新节点标记 
		a_s=f_i(s,1e18);//新流出量 
		if(a_s<=0)break;
		s_m+=a_s;//统计结果 
	} 
	printf("%lld",s_m);//输出结果 
	return 0;
}

Dinic

这时候，就需要介绍一下 Dinic 算法了。

Dinic 算法的精髓在于图的分层且支持反向弧，我们会发现在找 dfs 会不断更改之前错误的决策，或者更优的决策，例如下图：

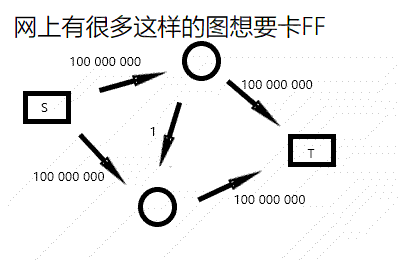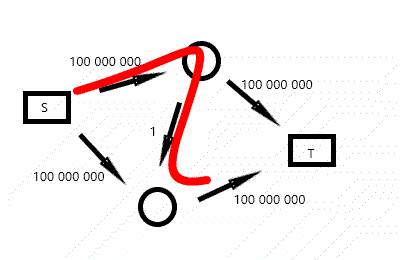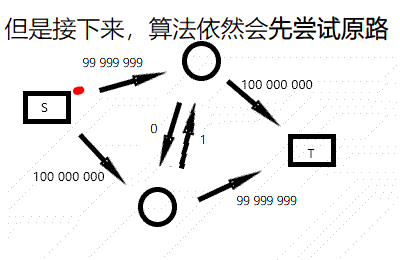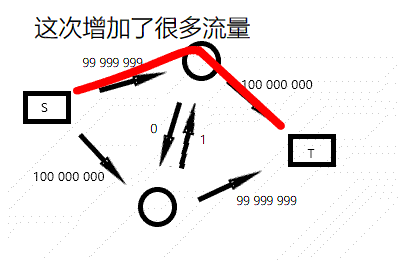
而 Dinic 解决这种方式采取的策略是，先跑一遍 Bfs 将整个图分层（给每个点打一个深度标志）。在 Dfs 的时候进行判段，如果深度刚好大 $1$，那么就可以流，否则不能流，更新后的图从新分层。

这样将长的路径流完后，不能再流了，在 Bfs 时，就直接“淘汰”不能用的点了，所以短路径也会被计算。

其他的和“普通代码”没有什么区别了。

Dinic代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<string>
#include<cctype>
#include<queue> 
using namespace std;
long long r_r(){//快读 
	long long x=0,f=1;
	char c=getchar();
	while(!isdigit(c)){
		if(c=='-')f=-1;
		c=getchar();
	}
	while(isdigit(c)){
		x=(x<<1)+(x<<3)+(c^48);
		c=getchar();
	}
	return x*f;
}
const int o_o=1e4+10;
int n=r_r(),m=r_r(),s=r_r(),t=r_r();
long long a_s=0;
struct po{
	int n_t;
	long long l;//边的流量 
	int v;//下一个节点 
}p_p[o_o];
int h_d[o_o],x_p=1;
void a_d(int u,int v,long long l){//建边 
	p_p[++x_p].v=v;
	p_p[x_p].l=l;
	p_p[x_p].n_t=h_d[u];
	h_d[u]=x_p;
}
int d_p[o_o];//深度
queue<int>s_s;
bool b_f(){//分层 
	memset(d_p,0,sizeof d_p);//清空深度 
	s_s.push(s);//从原点开始记录深度 
	d_p[s]=1;//深度初始化 
	while(!s_s.empty()){
		int k_k=s_s.front();
		s_s.pop();
		for(int i=h_d[k_k];i;i=p_p[i].n_t){//枚举连边 
			int v=p_p[i].v;
			if(p_p[i].l&&!d_p[v]){//没被遍历过并且有流向边 
				d_p[v]=d_p[k_k]+1;//赋值 
				s_s.push(v);//进入队列 
			}
		}
	}
	return d_p[t];//如果能流返回值 >1，否则返回 0 
}
long long d_f(int k,long long v_v){
	if(k==t)return v_v;//到达目的地，结束 
	long long s_m=0;//统计结果 
	for(int i=h_d[k];i;i=p_p[i].n_t){//枚举连边 
		int v=p_p[i].v;
		if(p_p[i].l&&d_p[v]==d_p[k]+1){//有流边，并且深度是下一层 
			long long a_s=d_f(v,min(p_p[i].l,v_v));//记录流边结果 
			p_p[i].l-=a_s;//更新流量 
			p_p[i^1].l+=a_s;//更新反向边流量 
			v_v-=a_s;//总流量分配一部分给成功流走的量 
			s_m+=a_s;//统计结果 
		}
	}
	if(s_m==0)d_p[k]=0;//没找到边可流，取消标记 
	return s_m;//返回结果 
}
int main(){
	for(int i=1;i<=m;i++){
		long long a=r_r(),b=r_r(),v=r_r();
		a_d(a,b,v);//建正向边 
		a_d(b,a,0);//建反向边 
	}
	while(b_f())a_s+=d_f(s,1e18);//统计结果 
	printf("%lld\n",a_s);//输出 
	return 0;
}