KMP
首先复习一下 kmp 算法。在 kmp 算法中,我们不断的“记忆”匹配位置,匹配失败后不重新匹配而是返回上次“记忆”的位置。这种“记忆”想法使得它的复杂度大大降低,而后面所说的 manchar 和扩展 kmp 也用到了这种想法。
manachar
嗯?这不 kmp 吗?和马拉车(manachar)有啥关系?
通过对比两者代码会发现:相似度极高。这是因为两者的做法虽然不同,但用到的“唤醒”“记忆”的方法却很相似。所以这里放到了一起,进行类比。
在马拉车中,在确定了一个回文串时,在当前回文串的回文中心后面并被当前回文串包含的回文中心,可以直接“唤醒”这个串的部分“回忆”,然后“记忆”这些“回忆”,在这些“记忆”上继续找即可,而不是重新寻寻找。扩展 kmp 的做法,和它极其相似,甚至代码结构都一模一样。
扩展KMP
题目让我们求 $z$ 权值和 $p$ 权值,不难发现 $z$ 权值要在自身身上“搞事情”,而 $p$ 权值是要在别人身上“搞事情”。这和 kmp 很相似,先自身找匹配,再让别人在自己这里找匹配。所以我们如果解决了自身的“问题”,别人的“问题”也就水到渠成了。
那么如何解决自己的“问题”呢?
题目让我们求得是字符串的所有后缀和原串的 LCP (最长公共前缀)。
我们遍历的过程就是下图:
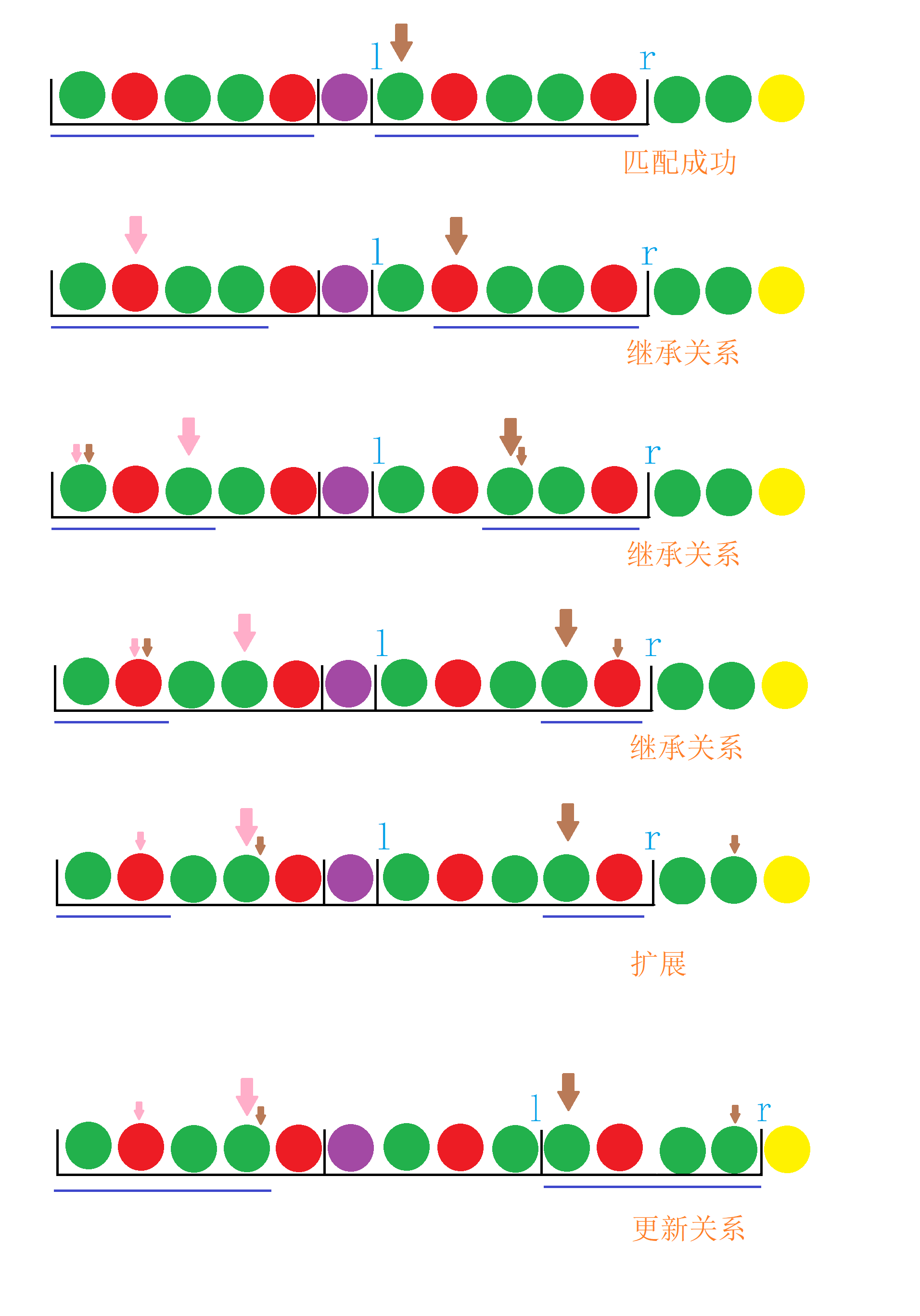
画图真费劲
第一个匹配成功是假设已经有匹配成功的段。大棕箭头是当前匹配的位置,大粉箭头是需要“唤醒”的“记忆”的位置。小粉箭头是“记忆”的大小($z$ 的值),小棕箭头先“读取”小粉箭头的“记忆”,在向后匹配,如果匹配成功结尾超出了目前的范围($[l,r]$之间的位置)要更新新的区间。
自己的“问题”解决了,处理别人的“问题”时,注意“唤醒”的是自己身上的“问题”的“记忆”。
代码
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<string>
#include<cctype>
#include<queue>
#include<vector>
using namespace std;
long long r_r(){//快读
long long x=0,f=1;
char c=getchar();
while(!isdigit(c)){
if(c=='-')f=-1;
c=getchar();
}
while(isdigit(c)){
x=(x<<1)+(x<<3)+(c^48);
c=getchar();
}
return x*f;
}
const int o_o=2e7+10;
int n_1,n_2,z[o_o],p[o_o];
char a_a[o_o],b_b[o_o];
int main(){
//读入字符串
char c=getchar();
while(c>'z'||c<'a')c=getchar();
while(c>='a'&&c<='z')a_a[++n_1]=c,c=getchar();
while(c>'z'||c<'a')c=getchar();
while(c>='a'&&c<='z')b_b[++n_2]=c,c=getchar();
//计算 Z 函数
z[1]=n_2;//第一位的 z 函数是原串长度
for(int i=2,l=0,r=0;i<=n_2;i++){//处理 z 权值
if(i<=r)z[i]=min(z[i-l+1],r-i+1);
while(i+z[i]<=n_2&&b_b[i+z[i]]==b_b[z[i]+1])++z[i];
if(i+z[i]-1>r)l=i,r=i+z[i]-1;
}
for(int i=1,l=0,r=0;i<=n_1;i++){//处理 p 权值
if(i<=r)p[i]=min(z[i-l+1],r-i+1);
while(i+p[i]<=n_1&&a_a[i+p[i]]==b_b[p[i]+1])++p[i];
if(i+p[i]-1>r)l=i,r=i+p[i]-1;
}
//计算结果
long long a_s=0;
for(int i=1;i<=n_2;i++)a_s^=1ll*i*(z[i]+1);
printf("%lld\n",a_s);
a_s=0;
for(int i=1;i<=n_1;i++)a_s^=1ll*i*(p[i]+1);
printf("%lld",a_s);
return 0;
}
