自然对数 e
很自然的一个常数(手动划掉)
再网上翻看了不少资料后,发现它并没有 $\pi$ 那么简单理解,更多的解释是一个值为 $2.71828182845904523536⋯$ 的常数,原因是发现不同方面都有它的身影。
我们从几个简单的例子入手,来大概了解一下它的“自然”。
增长极限
我们知道到银行存钱可以“生钱”,一般都会标明“复利”这一概念(通俗来讲:存多少钱,存几年,给多少钱)。那么如果增加涨钱,你会立刻得到很多钱么?
先在假设在 $1$ 个单位时间内,涨一次钱,每次涨一倍,那么用公式来表达:
$growth$ 代表增长率,现在我们让他增长的快一些,在 $1$ 个单位时间内,涨两次钱,那么平均 $\frac{1}{2}$ 个单位时间涨一次钱:
如果单位时间内涨 $10000$ 次,你会一夜暴富么?
嗯?怎么和想象的不一样?别急,如果我们单位时间内增长 $n$ 次,就有公式:
我们的 $e$ 出现了。根据自然增长,“涨”的次数越多,却不会很快的变多,而是有极限的 $e$(虽然它是无限不循环小数)。试想,这其实和现实中的细胞分裂道理相同,如果不加限制的快速增长,那世界会变成什么样子?所以这个常数确实非常“符合”“自然”。
注意:如果增加涨钱,确实会立刻的到很多钱,我们刚刚讨论的是增长率。
“加减术”
$2\sin A\times \cos B=\sin(A+B)+\sin(A-B)$
在很久很久以前如果要计算 $0.258819\times 0.984808$ 会是一个非常麻烦的事情,只能靠手算还要考虑进位。但是有了“加减术”后,可以在三角函数表中找到 $0.258819\approx \sin{15}^{\circ},0.984808\approx \cos{10}^{\circ}$。
那么就可以直接套公式了:
然后在三角函数表中找到:$\sin{25}^{\circ}\approx0.422618,\sin{5}^{\circ}\approx0.087156$,得出结果:$\approx0.254887$。
乘法运算变成了加法运算,是不是很神奇?和 FFT 的想法有些相似。
约翰.纳皮尔对数
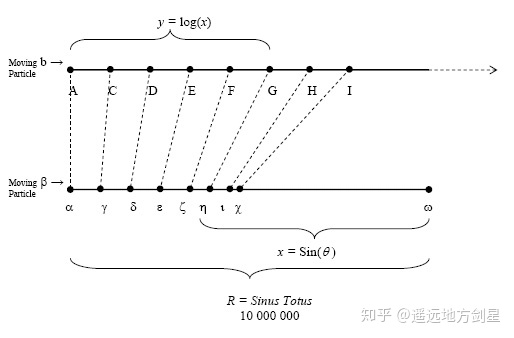
约翰.纳皮尔用运动来描述对数,一开始有两个粒子,分别在直线和线段上运动,在一开始时两个粒子的初速度相同,但是上面的 $b$ 粒子是匀速直线运动,下面的 $\beta$ 粒子的速度在数值上与它终点的距离相等。
经过对 $\beta$ 粒子速度的分析(需要微积分的知识,感兴趣的读者可以上网查阅相关内容),最后的到约翰.纳皮尔对数是 $\frac{1}{e}$ 为底的对数。
随后他有制成了 $10^7$ 的对数表(把圆等分成 $10^7$ 份的精确度),运用方法和“加减术”相同。单他简化的是开放乘法计算,类似于:$\sqrt{a\times b}$ 在表中分别找到 $a$ 对应的值 $k_a$,$b$ 对应的值 $k_b$,最后 $\sqrt{a\times b}=\frac{k_a+k_b}{2}$
无穷级数
相关公式
- 欧拉公式:
- 素数定理:
$\pi(x)$ 代表小于等于x的素数的个数。
- 高斯正态分布:
$\sigma$ 代表标准差,$\sigma^2$ 代表方差。
平时就当成和 $\pi$ 一样的常数处理就行了,只不过,它很“自然”。

