后缀数组

后缀数组

后缀数组释然给我们讲原串的每个元素在原串中的后缀按照字典序从大到小排序。

首先介绍几个数组的意义 sa，rank，height：

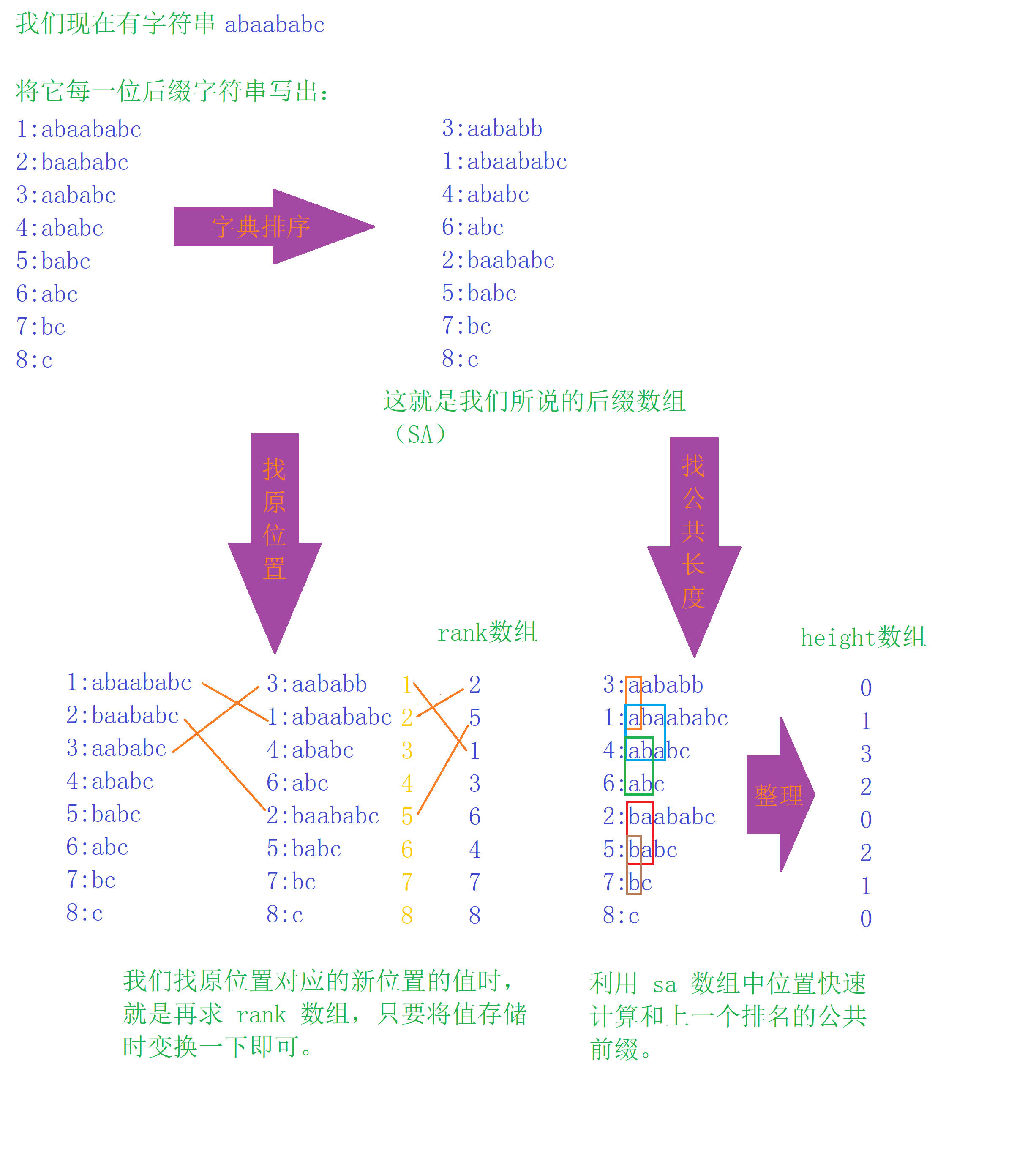
在排序的时候一般会用 $n^2\log{n}$ 的 string $\times $ sort，字符串比对的复杂度 $n$，共排序 $n$ 次，$n\log{n}$ 的排序复杂度。

但是它是字符串，是逐位匹配，所以可以用 基数排序 的思想，然后套一个倍增的思路。

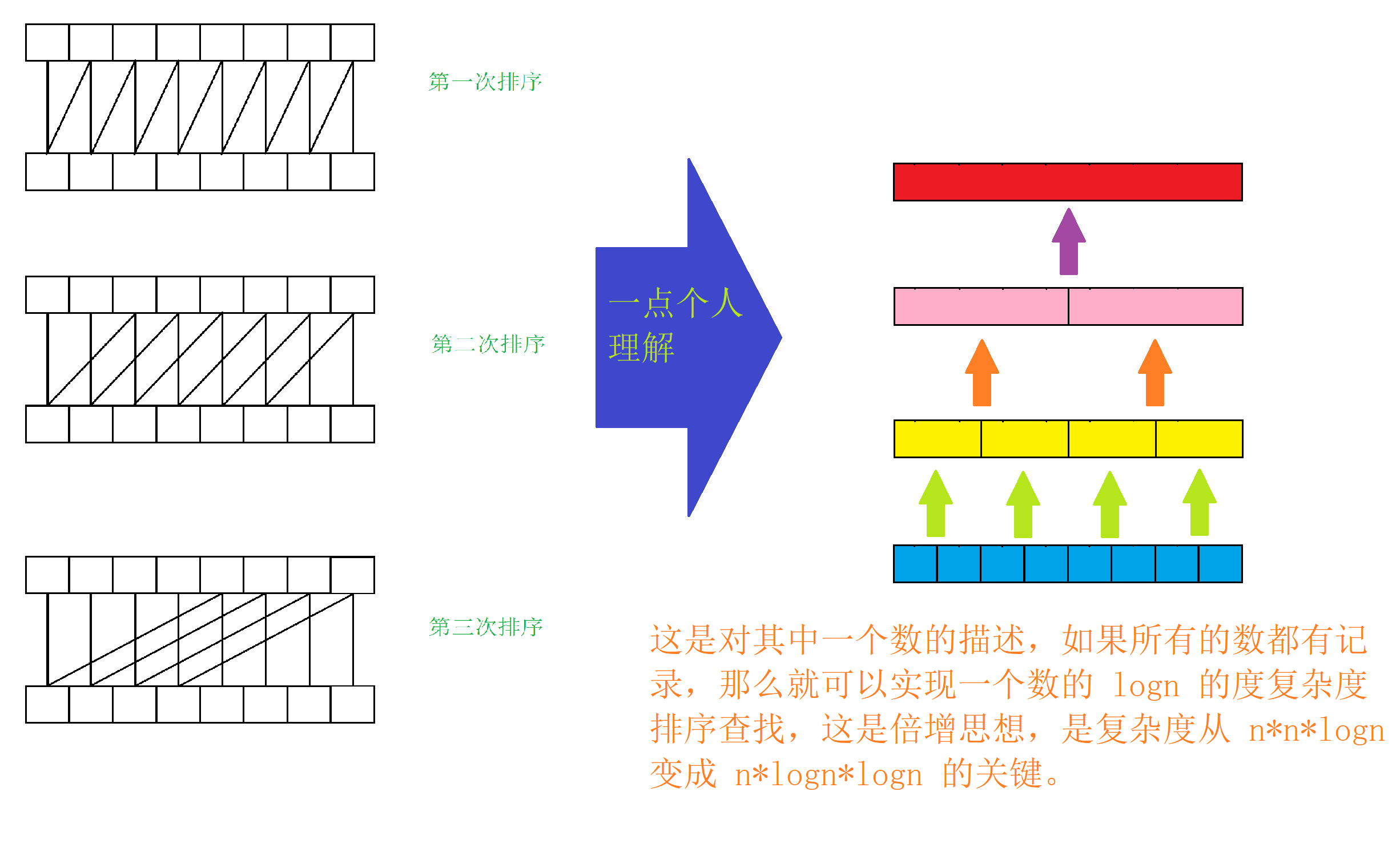
代码

#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<algorithm>
using namespace std;
const int o_o=1e6+10;
int s[o_o];//存原字符串 
int c_c[o_o];//存储字符串以某种元素开头的大致位置 
int s_i[o_o];//复制 s 字符串 
int s_y[o_o];//新的需要排序的元素 
int s_a[o_o];//根据字典排序后，按顺序的每个字符串的原位置 
int r_k[o_o];//排好序后，原位置的字符串去到的新的位置 
int g_q[o_o];//相邻的两个串的最长公前缀（排好序的字符串） 
int n,m=66;
int f_n(char c){//字符重新赋值权值 
  if(isdigit(c))return c-'0'+1;
  if(isupper(c))return c-'A'+12;
  if(islower(c))return c-'a'+39;
}
void h_z(){
  for(int i=0;i<n;i++)s_i[i]=s[i],c_c[s_i[i]]++;//将 s 复制到 s_i 中，并用 c_c 记录各种字符开头的数量 
  for(int i=1;i<m;i++)c_c[i]+=c_c[i-1];//前缀和，计算每种字符开头的字符串的排名的大致范围（c_c[i-1]-1~c_c[i]） 
  for(int i=n-1;i>=0;i--)s_a[--c_c[s_i[i]]]=i;//第一次排序 
  for(int k=1;k<=n;k<<=1){//每次比较的长度翻一倍 
    int t_p=0;//需要比较元素数组的下标 
    for(int i=n-k;i<n;i++)s_y[t_p++]=i;//将需要新比较的元素下标存储 
    for(int i=0;i<n;i++)//从头遍历 
      if(s_a[i]>=k)//上一次排序后，排名在 k 及之后的数 
        s_y[t_p++]=s_a[i]-k;//将排名后元素中心赋值排名并存储  
    
    for(int i=0;i<n;i++)c_c[i]=0;//初始化 
    for(int i=0;i<n;i++)c_c[s_i[i]]++;//统计每种元素开头数量 
    for(int i=1;i<m;i++)c_c[i]+=c_c[i-1];//前缀和，每种元素排名的范围 
    for(int i=n-1;i>=0;i--)s_a[--c_c[s_i[s_y[i]]]]=s_y[i];//排序 
    
    swap(s_i,s_y);//交换 s_y，s_i 数组 
    //比较新的排名时需要用到旧的位置来确定最后的排名 
    
    t_p=1;//初始化数组下标 
    s_i[s_a[0]]=0;//初始化最高排名 
    
    for(int i=1;i<n;i++)//全部遍历 
      s_i[s_a[i]]=s_y[s_a[i-1]]==s_y[s_a[i]]&&((s_a[i]+k>n?-1:s_y[s_a[i]+k])==(s_a[i-1]+k>n?-1:s_y[s_a[i-1]+k]))?t_p-1:t_p++;
    //生成下一次排序的关键字
     
    if(t_p>=n)break;//超过原字符串长度 
    m=t_p;//更新元素总数 
  }
}
void g_t(){//找排好序后的最长公共前缀 
  for(int i=0;i<n;i++)r_k[s_a[i]]=i;//排好序后，原位置的字符串去到的新的位置 
  int k=0;//初始化公共长度 
  g_q[0]=0;//最开始的公共前缀一定是 0 
  for(int i=0;i<n;i++){
    if(!r_k[i])continue;//去 1 的位置的数直接跳过 
    if(k)k--;//相邻的字符串至少 -1 公共长度 
    int j=s_a[r_k[i]-1];//获取排序后的 s_a 的当前下标 
    while(i+k<n&&j+k<n&&s[i+k]==s[j+k])k++;//在字符串内并且可以进行更长的匹配字符串 
    g_q[r_k[i]]=k;//按排好序后，原位置的字符串去到的新的位置，记录匹配长度 
  }
}
int main(){
  char c=getchar();
  while(!isdigit(c)&&!isupper(c)&&!islower(c))c=getchar();//不是数字，大小写 
  while(isdigit(c)||isupper(c)||islower(c)){//读入字符串 
    s[n++]=f_n(c);
    c=getchar();
  }
  h_z();//搞 s_a 
  g_t();//搞 r_k，g_q 
  for(int i=0;i<n;i++)printf("%d ",s_a[i]+1);//输出根据字典排序后，按顺序的每个字符串的原位置 
  puts("");
  for(int i=0;i<n;i++)printf("%d ",r_k[i]+1);//输出排好序后，原位置的字符串去到的新的位置  
  puts("");
  for(int i=0;i<n;i++)printf("%d ",g_q[i]);//输出相邻的两个串的最长公前缀（排好序的字符串） 
  puts("");
  return 0;
}