重要极限形式&无穷小比较&函数连续性

前置文章：

数列极限&极限基础

函数极限&极限运算&极限存在准则

自然对数e

重要极限形式

一般我们通过正常的运算来凑出形式，求解。

值为 $1$

$$\lim_{x\to 0}{\frac{\sin{x}}{x}}=1$$

• 练习（求值）：

• $1$:

$$\lim_{n\to \infty}{n\sin{\frac{2}{n}}}$$ $$=\lim_{n\to \infty}{\frac{ {\sin{\frac{2}{n}}}}{\frac{1}{n}}}=2\lim_{n\to \infty}{\frac{ {\sin{\frac{2}{n}}}}{\frac{2}{n}}}$$ $$\because n \to \infty$$ $$\therefore \frac{2}{n} \to 0$$ $$=2\lim_{\frac{2}{n}\to 0}{\frac{ {\sin{\frac{2}{n}}}}{\frac{2}{n}}}$$ $$=2$$

• $2$:

$$\lim_{x\to 0}{\frac{\tan{x}}{x}}$$ $$=\lim_{x\to 0}{\frac{\sin{x}}{x}\frac{1}{\cos{x}}}$$ $$\because \lim_{x\to 0}{\cos{x}}=1$$ $$\therefore \lim_{x\to 0}{\frac{1}{\cos{x}}}=1$$ $$\lim_{x\to 0}{\frac{\sin{x}}{x}\frac{1}{\cos{x}}}=1$$

值为 $e$

$$\lim_{x\to \infty}{(1+\frac{1}{x})^x}=e$$

• 练习（求值）：

• $1$：

$$\lim_{x\to \infty}{(1+\frac{2}{x})^x}$$ $$=\lim_{x\to \infty}{((1+\frac{1}{\frac{x}{2}})^{\frac{x}{2}})^2}$$ $$=\lim_{\frac{x}{2}\to \infty}{((1+\frac{1}{\frac{x}{2}})^{\frac{x}{2}})^2}=e^2$$

• $2$：

$$\lim_{x\to \infty}{(1-\frac{1}{x})^x}$$

将分母化为负数，凑指数后得到结构，直接计算即可：

$$=e^{-1}=\frac{1}{e}$$

• $3$：

$$\lim_{x\to \infty}{(\frac{x+2}{x-1})^x}$$ $$=\lim_{x \to \infty}{(\frac{\frac{x+2}{x}}{\frac{x-1}{x}})^x}$$ $$=\lim_{x \to \infty}{(\frac{1+\frac{2}{x}}{1-\frac{1}{x}}})^x$$ $$=\lim_{x \to \infty}{\frac{((1+\frac{1}{\frac{x}{2}})^{\frac{x}{2}})^2}{((1-\frac{1}{-x})^{-x})^{-1}}}$$ $$=\frac{e^2}{e^{-1}}=e^3$$

无穷小比较

设：

$$\lim{g(x)=0},\lim{f(x)}=0(x\not=0)$$

• $1$：$f(x)$ 比 $g(x)$ 高阶无穷小 $f(x)=o(g(x))$，

$$\lim_{x\to 0}{\frac{f(x)}{g(x)}}=0$$

• $2$：$f(x)$ 比 $g(x)$ 低阶无穷小 $o(f(x))=g(x)$，

$$\lim_{x\to 0}{\frac{f(x)}{g(x)}}=\infty$$

• $3$：$f(x)$ 比 $g(x)$ 同阶无穷小 $f(x)=cg(x)$，其中 $c$ 是常数，

$$\lim_{x\to 0}{\frac{f(x)}{g(x)}}=c$$

• $4$：$f(x)$ 比 $g(x)$ 等价无穷小 $f(x)=g(x)$，$c=1$ 时，

$$\lim_{x\to 0}{\frac{f(x)}{g(x)}}=1$$

记作：$f(x)\sim g(x)$

重点比较

• $1$：$\ln(1+x)\sim x(x\to 0)$

$$\lim_{x\to 0}{\frac{\ln{(1+x)}}{x}}=\lim_{x\to 0}{\ln{(1+x)}^{\frac{1}{x}}}=\ln{e}=1$$

• $2$：$e^x-1\sim x$

$$\lim_{x\to 0}{\frac{e^x-1}{x}}$$

设：$k=e^x-1$，则有 $e^x=k+1$，$x=\ln{(k+1)}$

$$=\lim_{k\to 0}{\frac{k}{\ln{(k+1)}}}=1$$

可以结合第一个比较来看。

• $3$：$\sqrt[n]{1+x}-1\sim \frac{x}{n}$

$$\lim_{x\to 0}{\frac{(1+x)^{\frac{1}{n}}}{\frac{x}{n}}}$$ $$\because a^n-1=(a-1)(a^{n-1}+a^{n-2}+…+a+1)$$ $$\therefore a^n=(a-1)(a^{n-1}+a^{n-2}+…+a+1)+1$$ $$\therefore a^{\frac{1}{n}}=(a-1)(a^{\frac{n-1}{n}}+a^{\frac{n-2}{n}}+…+a^{\frac{1}{n}}+1)+1$$

设 $a=x+1$

$$=\lim_{x\to 0}{\frac{1+x-1}{\frac{x}{n}((1+x)^{\frac{n-1}{n}}+…+(1+x)^{\frac{1}{n}}+1)}}$$ $$\because x\to 0$$ $$\therefore (1+x)^{\frac{n-1}{n}}=(1+0)^{\frac{n-1}{n}}=1$$ $$=\lim_{x\to 0}\frac{x}{\frac{x}{n}\times n}$$ $$=1$$

无穷小替换

$$(x\to 0):\sin{x}\sim x,\tan{x}\sim x$$

如果：$f_1(x)\sim f_2(x),g_1(x)\sim g_2(x),\lim{\frac{f_2(x)}{g_2(x)}}$ 存在。

$$\lim{\frac{f_1(x)}{g_1(x)}}=\lim{\frac{f_2(x)}{g_2(x)}}$$

（定理）

• 两个无穷小之比才能用，$\lim(f_1(x)+g_1(x))\not=\lim(f_2(x)+g_2(x))$。

• 分子或分母是因子乘积（无穷小），选部分因子替换。

$$\lim_{x\to 0}{\frac{\sin{2x}}{x^3+3x}}=\lim_{x\to 0}{\frac{2x}{x^3+3x}}=\frac{2}{x^2+3}=\frac{2}{3}$$ $$\lim_{x\to 0}{\frac{(e^x-1)\sin x}{1-\cos x}}=\lim_{x\to 0}{\frac{x\times x}{\frac{1}{2}x^2}}=2$$

函数连续性

$$\Delta y=f(x_0+\Delta x)-f(x_0)$$

$$\Delta x\to 0,\Delta y\to 0$$

$$\Delta x\to 0,\Delta y \not\to 0$$

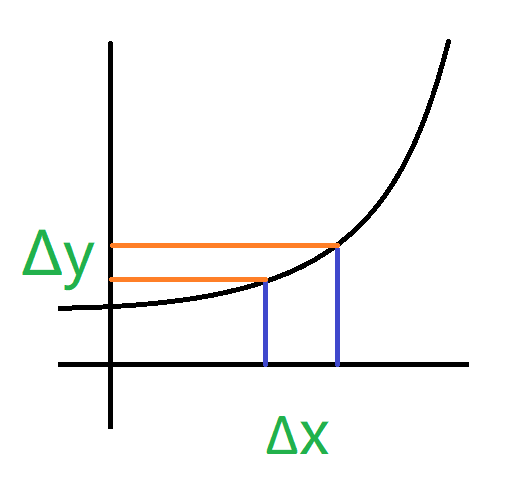
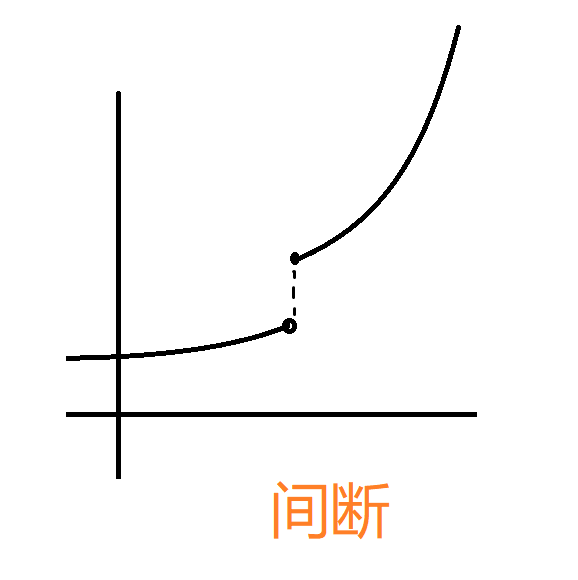
$f(x)$ 在 $x_0$ 领域内有定义，$\Delta x\to 0,\Delta y\to 0$

$$\lim_{\Delta x\to 0}{\Delta y=\lim_{\Delta x\to 0}}{(f(x_0+\Delta x)-f(x))}=0$$

在点上连续（某点连续定义）。

• 左连续：$(x_o-\delta,x_o]$

$$\lim_{x\to x^{-}}{f(x)=f(x_0)}$$

• 右连续：$[x_o,x_o+\delta)$

$$\lim_{x\to x^{+}}{f(x)=f(x_0)}$$

区间连续：

$$[1,2]= \begin{cases} (1,2)\\ 1\\ 2 \end{cases}$$

$(1,2)$ 连续，$1$ 右连续，$2$ 左连续。

$$\lim_{x\to x_0}f(x)=f(x_0)$$

间断点：

• $x_0$ 有定义

• $x\to x_0$ ，$f(x)$ 有极限

• 极限 $= f(x_0)$

间断点

• 第一类

当左右极限相等，则称为可去间断点；左右极限不等，则称为跳跃间断点。

可取间断点：

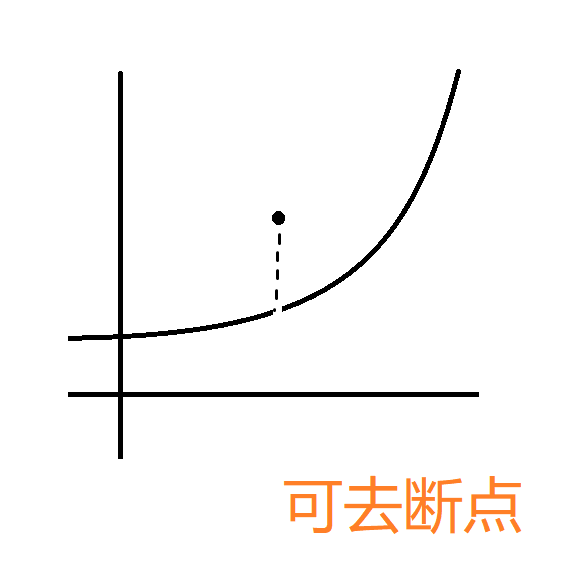
跳跃间断点：

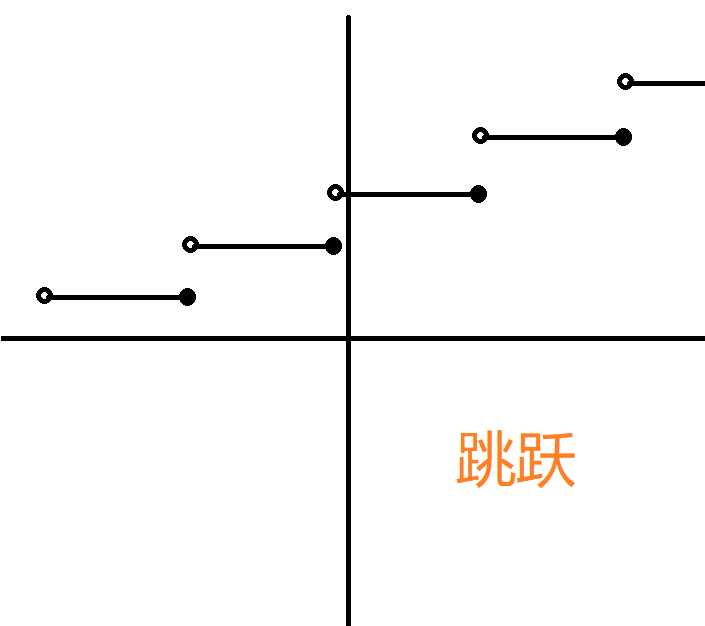
• 第二类

左右几点至少有一个不存在。

无穷间断（$y=\frac{1}{x},x=0$）：

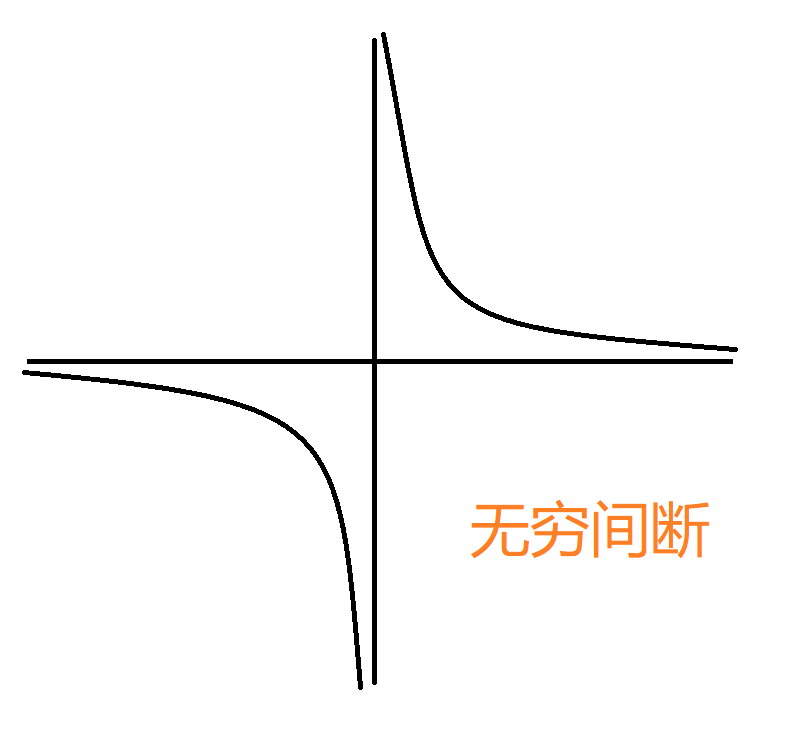
振荡：

举例：

$$y= \begin{cases} \sin{\frac{1}{x}},(x\not =0)\\ 0,(x=0) \end{cases}$$

图示也算是一种振荡间断点。

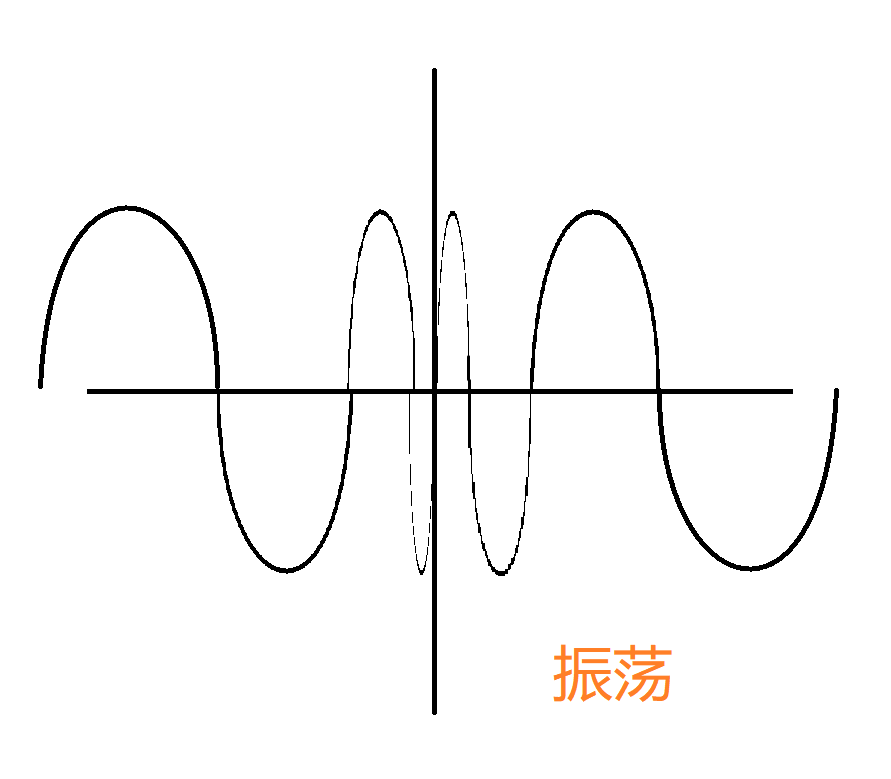
• 练习：

$$y=\lim_{n \to \infty}{\frac{1}{1+x^n}},x=1$$ $$y= \begin{cases} 1,(0\leqslant x < 1)\\ \frac{1}{2},(x=1)\\ 0,(x>1) \end{cases}$$

第一类间断点。

四则运算

$$g(x)\pm f(x)$$ $$g(x)f(x)$$ $$\frac{f(x)}{g(x)}$$

其中：

$$(g(x)\not = 0)$$

连续多项式：

$$a_{0}x^n+a_{1}x^{n-1}+…+a_{n-1}x+a_{n}(-\infty,+\infty)$$

分式：多项式除多项式

复合多项式：

$$y=f(k),k=g(x)$$

分别连续，极限可以换到另一个函数中（括号内）。

反函数

练习：

$$f(x)= \begin{cases} a+x,(x\leqslant 0)(-\infty,0]\\ x^2+1,(0 < x < 1),(0,1)\\ \frac{b}{x},(x \geqslant 1),[1,+\infty)) \end{cases}$$

$x=0$ 时，$f(0)=a$

$$\lim_{x\to 0^{-}}{f(x)}=a$$ $$\lim_{x\to 0^{+}}{f(x)}=1$$ $$a=1$$

$x=1$ 时，$f(1)=b$

$$\lim_{x\to 1^{-}}{f(x)}=2$$ $$\lim_{x\to 1^{+}}{f(x)}=b$$ $$b=2$$

闭区间上的连续性质

• （有界性）$[a,b]$ 连续有界

• （最值性）有最大最小值

• （介值性）$x_1 < k < x_2$ 必定存在 $f(x_0)=k$

零点存在定理

$[a,b]$ 连续，$f(a)f(b) < 0$

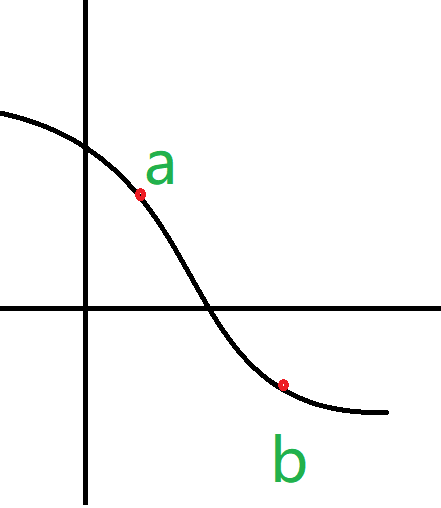
在 $[a,b]$ 有一点 $x$，$f(x)=0$

• 练习：

$e_{3x}-x=2$，求 $(0,1)$ 至少有一个实根。

$f(x)=e^{3x}-x-2=0$ 在 $[0,1]$ 连续。

$f(0)=1-2=-1,f(1)=e^3-3>0$

根据零点存在定理，$\exists x \in(0,1),f(x)=e^{3x}-x-2=0$