中值定理&泰勒展开&洛必达法则&函数凹凸及绘制

微分基础

中值定理

费马引理

$f(x)$ 在 $x_0$，$U(x_0)$ 有定义，在 $x_0$ 处可导，如 $f(x)\le f(x_0),\forall x\in U(x_0)$，则 $f^{‘}{(x_0)}=0$。

设 $x\in U(x_0),f(x)\le f(x_0)$

$$x_0+\Delta x\in U(x_0)$$ $$f(x_0+\Delta x)\le f(x_0)$$ $$f^{'}_{-}{x_0}=\lim_{\Delta x\to 0^{-}}{\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}}\ge0$$ $$f^{'}_{+}{x_0}=\lim_{\Delta x\to 0^{+}}{\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}}\ge0$$ $$f^{'}{(x_0)}=0$$

驻点：导数为 $0$ 的点。

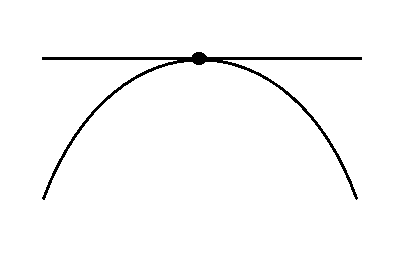
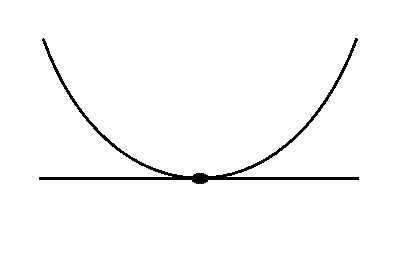
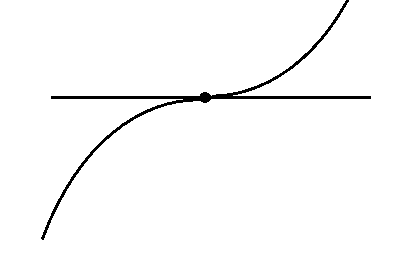
罗尔中值定理

$f(x)$ 满足：

• 在 $[a,b]$ 连续

• $(a,b)$ 可导

• $f(a)=f(b)$

则至少 $\exists \xi\in(a,b),f^{‘}{(\xi)}=0$

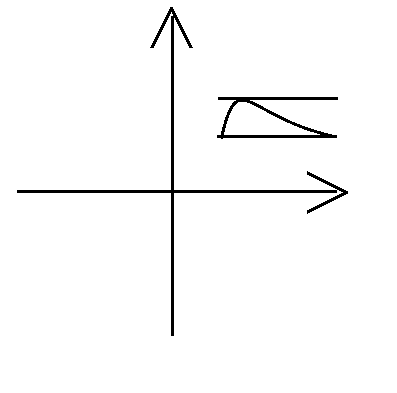
（通俗：两点的 $y$ 值相等，不管中间的线的路径是什么，至少有一点的斜率为 $0$）

拉格朗日中值定理

• $[a,b]$ 连续

• $(a,b)$ 可导

$(a,b)$ 至少有一点 $f(b)-f(a)=f^{‘}{(\xi)}(b-a)$

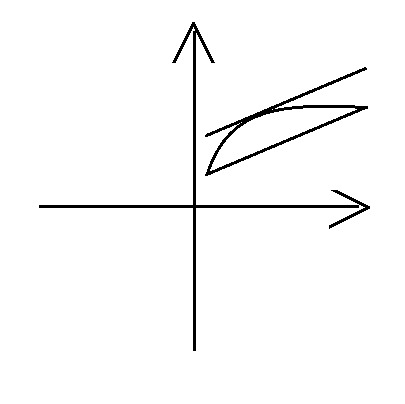
（通俗：有两点，不管中间的线的路径是什么，至少有一点的斜率与两点组成的一次函数的斜率相同）

• 定理：$f(x)$ 在区间 $I$ 连续，$I$ 内可导，且导数恒为 $0$，$f(x)=c$。

$$\forall x_1.x_2,\xi \in(x_1,x_2)$$ $$f(x_1)-f(x_2)=f^{'}{(\xi)}(x_1-x_2)$$ $$f(x_1)=f(x_2)$$ $$f(x)=c$$

（$c$ 为常数。）

柯西中值定理

• 若 $f(x)$ 和 $F(x)$

• $[a,b]$ 连续

• $(a,b)$ 可导

• $\forall x\in (a,b),F^{‘}{(x)}\not=0$

至少有一点 $\xi$

$$\frac{f(b)-f(a)}{F(b)-F(a)}=\frac{f^{'}{(\xi)}}{F^{'}{(\xi)}}$$

• 总结：

• 罗尔中值定理： $f^{‘}{(\xi)}=0$

• 拉格朗日中值定理：$f^{‘}{(\xi)}=\dfrac{f(b)-f(a)}{b-a}$

• 柯西中值定理：$\dfrac{f(b)-f(a)}{F(b)-F(a)}=\dfrac{f^{‘}{(\xi)}}{F^{‘}{(\xi)}}$

泰勒展开

$$f(x)-f(x_0)\approx f^{'}{(x_0)}(x-x_0)$$ $$dy\approx f^{'}{(x_0)}dx$$ $$f(x)\approx f(x_0)+f^{'}{(x_0)}(x-x_0)$$

• 定理：$f(x)$ 表示成 $x-x_0$ 的 $n$ 的多项式 $+R_n(x)$（余项）

$$f(x)=f(x_0)+\frac{f^{'}{(x_0)}(x-x_0)}{1!}+\frac{f^{''}{(x_0)}(x-x_0)^2}{2!}+…+\frac{f^{n}{(x_0)}(x-x_0)^{n}}{n!}+R_n(x)$$ $$R_n(x)=\frac{f^{(n+1)}{(\xi)}(x-x_0)^{n+1}}{(n+1)!}$$

$\xi$ 在 $x_0$ 和 $x$ 之间（拉格朗日型余项）。

$n$ 阶马克劳林公式

自然对数 $e$

$$f(x)=e^x$$ $$f^{'}{(x)}=f^{''}{(x)}=…=f^{(n)}{(x)}=e^x$$ $$f^{'}{(0)}=f^{''}{(0)}=…=f^{(n)}{(0)}=1$$ $$e^x=1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+…+\frac{x^n}{n!}+R_n(x)$$ $$R_n(x)=\frac{e^{\theta x}x^{n+1}}{(n+1)!}$$ $$(0 < \theta < 1)e^{\theta x}=e^{\xi}(0 < \xi < x)$$ $$|R_n(x)|<\dfrac{e^{|x|}x^{n+1}}{(n+1)!}$$

$e^{|x|}$ 是定值，$x^{n+1}\to 0(x\to 0)$，$(n+1)!$ 非常大。

$$e^x\approx 1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+…+\frac{x^n}{n!}$$

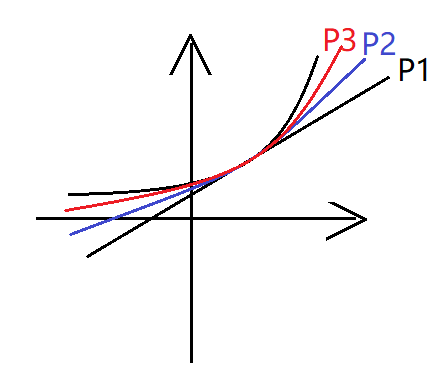
（最上面的黑线是 $y=e^x$）

• $$f(x)=\sin x$$

$$\sin x=x-\frac{1}{3!}x^3+\frac{1}{5!}x^5+…+\frac{(-1)^{m-1}}{(2m-1)!}x^{2m-1}+R_{2m}{(x)}$$

洛必达法则

$$f(x)\to 0,g(x) \to 0,\frac{f(x)}{g(x)},\frac{0}{0}$$ $$f(x)\to \infty,g(x) \to \infty,\frac{f(x)}{g(x)},\frac{\infty}{\infty}$$

若 $f(x),g(x)$

$$\lim_{x\to x_0}{f(x)}=\lim_{x-x_0}{g(x)}=0$$

在 $x_0$ 的邻域内（$x_0$ 可除外）可导，$g^{‘}{(x)}=0$

$$\lim_{x-x_0}{\frac{f^{'}{(x)}}{g^{'}{(x)}}}=a$$

或者 $\infty$

$$\lim_{x-x_0}{\frac{f{(x)}}{g{(x)}}}=\lim_{x-x_0}{\frac{f^{'}{(x)}}{g^{'}{(x)}}}=a$$

或者 $\infty$

证（柯西中值定理）：

• $f(x),g(x)$ 在 $[a,b]$ 连续

• $f(x),g(x)$ 在 $(a,b)$ 可导 $(g^{‘}{(x)}\not =0)$

$$\frac{f(b)-f(a)}{g(b)-g(a)}=\frac{f^{'}{(\xi)}}{g^{'}{(\xi)}}$$

设在 $[x_0,x]$，$f(x_0)=g(x_0)=0$。

$$\frac{f(x)}{g(x)}(x\to 0)=\frac{f(x)-f(x_0)}{g(x)-g(x_0)}=\frac{f^{'}{(x)}}{g^{'}{(x)}}$$ $$\xi \in (x_0,x)$$

• 连等：

$$x\to x_0,\xi \to x$$ $$\lim_{x\to x_0}\frac{f(x)}{g(x)}=\lim_{x\to x_0}\frac{f^{'}{(x)}}{g^{'}{(x)}}=\lim_{x\to x_0}\frac{f^{''}{(x)}}{g^{''}{(x)}}=…$$

注意：只有 $\frac{0}{0}$ 和 $\frac{\infty}{\infty}$ 时才能用。

• 练习：

• $1$：

$$\lim_{x\to x_0}\frac{x-\sin x}{x^3}=\lim_{x\to x_0}\frac{1-\cos x}{3x^2}=\lim_{x\to x_0}\frac{\sin x}{6x}=\frac{1}{6}$$ $$\lim_{x\to 0}{\frac{\sin x}{x}}=\lim_{x\to 0}{\cos x}=1$$

• $2$：

$$\lim_{x\to 1}\frac{x^3-3x+2}{x^3-x^2-x+1}=\lim_{x\to 1}\frac{3x^2-3}{3x^2-2x-1}=\lim_{x\to 1}{\frac{6x}{6x-2}}=\frac{3}{2}$$

• $3$：

$$\lim_{x\to 0}\frac{\ln{(1+x)}}{x^2}=\lim_{x\to 0}\frac{\frac{1}{x+1}}{2x}=\lim_{x\to 0}\frac{1}{2x(x+1)}=\infty$$

• $\frac{\infty}{\infty}$ 和 $\frac{0}{0}$ 没有本质区别。

$$\lim_{x\to +\infty}\frac{x^4}{e^x}=\lim_{x\to +\infty}\frac{\frac{1}{e^x}}{\frac{1}{x^4}}$$

从 $\frac{\infty}{\infty}$ 转换到 $\frac{0}{0}$

• $\frac{\infty}{\infty}$

• $1$：

$$\lim_{x\to +\infty}{\frac{\ln x}{\sqrt{x}}}=\lim_{x\to +\infty}{\frac{\frac{1}{x}}{\frac{1}{2\sqrt{x}}}}=\lim_{x\to +\infty}{\frac{2}{\sqrt{x}}}=0$$

• $2$：

$a>0,n$ 是正整数。

$$\lim_{x\to +\infty}{\frac{x^n}{e^{a x}}}=\lim_{x\to +\infty}{\frac{nx^{n-1}}{ae^{a x}}}=\lim_{x\to +\infty}{\frac{n(n-1)x^{n-2}}{a^2e^{a x}}}=…=\lim_{x\to +\infty}{\frac{n!}{a^ne^{a x}}}=0$$

• $3$：

$a>0,n$ 是实数。

设 $n=2.5$：

$$\lim_{x\to +\infty}{\frac{x^{2.5}}{e^{a x}}}=\lim_{x\to +\infty}{\frac{(2.5)x^{1.5}}{ae^{a x}}}=\lim_{x\to +\infty}{\frac{(2.5)\times(1.5)x^{0.5}}{a^2e^{a x}}}=\lim_{x\to +\infty}{\frac{2.5\times 1.5\times 0.5}{x^{0.5}a^3e^{a x}}}=0$$

• 只有 $\frac{0}{0}$ 和 $\frac{\infty}{\infty}$ 才能用。

• 与重要极限，等价无穷小替换结合

• 若 $\lim{\dfrac{f^{‘}{(x)}}{g^{‘}{(x)}}=a}$ 或 $\infty$ 时。

$$\lim{\dfrac{f{(x)}}{g{(x)}}}=\lim{\dfrac{f^{'}{(x)}}{g^{'}{(x)}}}$$

但若 $\lim{\dfrac{f^{‘}{(x)}}{g^{‘}{(x)}}}$ 不存在，也不是 $\infty$ 时，不能说明 $\lim{\dfrac{f{(x)}}{g{(x)}}}$ 不存在，要换方法。

• 等价无穷小替换（$sin x\sim x$）只有除时可以换！：

$$\lim_{x\to 0}{\frac{x-\sin x}{x^2\sin x}}=\lim_{x\to 0}{\frac{x-\sin x}{x^3}}=\lim_{x\to 0}{\frac{1-\cos x}{3x^2}}=\frac{1}{6}$$

• 先处理（注意 $x\to \infty$）：

$$\lim_{x\to \infty}{\frac{x+\sin x}{x}}=1+\lim_{x\to \infty}{\frac{\sin x}{x}}=1$$

• 约分：

$$\lim_{x\to 0}{x^2e^{\frac{1}{x^2}}}=\lim_{x\to 0}{\frac{e^{\frac{1}{x^2}}}{\frac{1}{x^2}}}=\lim_{x\to 0}{\frac{-\frac{2}{x^3}e^{\frac{1}{x^2}}}{-\frac{2}{x^3}}}=\lim_{x\to 0}{e^{\frac{1}{x^2}}}=\infty$$

• 无穷小替换：

$$\lim_{x\to 0^{+}}{x^x}=\lim_{x\to 0^{+}}{e^{x\ln x}}=\lim_{x\to 0^{+}}{e^{\frac{\ln x}{\frac{1}{x}}}}=\lim_{x\to 0^{+}}{e^{\frac{\frac{1}{x}}{-\frac{1}{x^2}}}}=e^0=1$$

函数凹凸性

单调性判断

单调性，$f^{‘}{(x)} > 0$ 增函数，$f^{‘}{(x)} < 0$ 减函数，$f^{‘}{(x)}\ge 0$ 等号在个别点成立。

• $1$：

$$y=x-\sin x$$

定义域：$[0,2\pi]$

$$y^{'}=1-\cos x > 0$$

$(0,2x)$ 增

• $2$：

$$y=e^x-x-1,y^{'}=e^x-1$$

$x<0,y^{‘}<0$ 减

$x>0,y^{‘}>0$ 增

• $3$：

$$y=\sqrt[3]{x^2}=x^{\frac{2}{3}}$$

定义域 $(-\infty,\infty)$

$$x\not=0,y^{'}=\frac{2}{3}\frac{1}{\sqrt[3]{x}}$$

$x<0,y^{‘}<0$ 减

$x>0,y^{‘}>0$ 增

$x=0$ 分界点。

$$\lim_{\Delta x\to 0^{-}}{\frac{\Delta x^{\frac{2}{3}}-0}{\Delta x}}=\lim_{\Delta x\to 0^{-}}{\frac{1}{\Delta x^{\frac{1}{3}}}}=-\infty$$ $$\lim_{\Delta x\to 0^{+}}{\frac{\Delta x^{\frac{2}{3}}-0}{\Delta x}}=\lim_{\Delta x\to 0^{+}}{\frac{1}{\Delta x^{\frac{1}{3}}}}=+\infty$$

导数不存在。

分界点：

• $f^{‘}{(x)}=0$ 驻点。

• 导数不存在。

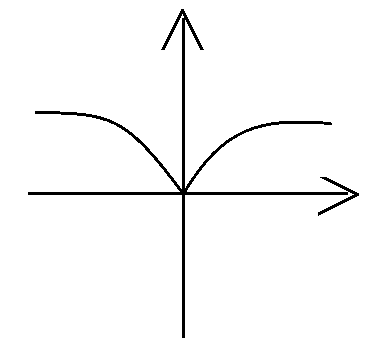
凹凸性

凹：

$$f(\frac{x_1+x_2}{2})<\frac{f(x_1)+f(x_2)}{2}$$

凸：

$$f(\frac{x_1+x_2}{2})>\frac{f(x_1)+f(x_2)}{2}$$

$f^{‘}{(x)}$ 增，$f^{‘’}{(x)}>0$ 凹。

$f^{‘}{(x)}$ 减，$f^{‘’}{(x)}<0$ 凸。

• 推导：

$f^{‘’}{(x)}>0,x_1,x_2,x_1 < x_2,x_0=\frac{x_1+x_2}{2}$

在 $[x_1,x_0],f^{‘}{(\xi_1)}=\frac{f(b)-f(a)}{b-a}$

$$f{(x_0)}-f(x_1)=f^{'}{(\xi_1)}(x_0-x_1)$$ $$\xi_1\in(x_1,x_0)$$

在 $[x_0,x_2],f^{‘}{(\xi_2)}=\frac{f(b)-f(a)}{b-a}$

$$f{(x_2)}-f(x_0)=f^{'}{(\xi_2)}(x_2-x_0)$$ $$\xi_2\in(x_0,x_2)$$ $$2f(x_0)-(f{(x_1)}+f{(x_2)})=\frac{1}{2}(f^{'}{(\xi_1)}-f^{'}{(\xi_2)})(x_2-x_1)$$ $$=\frac{1}{2}(x_2-x_1)f^{''}{(\eta)}(\xi_1-\xi_2)$$ $$(x_2-x_1)>0,f^{''}{(\eta)}>0,(\xi_1-\xi_2)<0$$ $$\frac{1}{2}(x_2-x_1)f^{''}{(\eta)}(\xi_1-\xi_2)<0$$ $$2f(x_0)-(f{(x_1)}+f{(x_2)})<0$$ $$f(\frac{x_1+x_2}{2})<\frac{f(x_1)+f(x_2)}{2}$$

• 拐点：凹凸性质改变，$f^{‘’}{(x)}=0$ 或 $f^{‘’}{(x)}$ 不存在。

• 练习：

$$y=xe^{-x}$$

定义域：$[-\infty,+\infty]$

$$y^{'}=e^{-x}(1-x),y^{''}=e^{-x}(x-2)$$ $$x=2,f^{''}{(x)}=0$$

列表作图：

$x$	$(-\infty,2)$	$2$	$(2,+\infty)$
$y^{‘’}$	$-$	0	$+$
$y$	凸		凹

极大值，极小值

$$U(x_0),\forall x\in U(x_0),f(x)<f(x_0)$$

$f(x_0)$ 极大值，$x_0$ 极大值点。

$f(x)>f(x_0)$，$f(x_0)$ 极小值，$x_0$ 极小值点。局部，极值不唯一，不相等。

定理：$f(x_0)$ 在 $x_0$ 可导，且在 $x_0$ 取极值，$f^{‘}{(x_0)}=0$ 。

证明：设取极大值，$x_0$ 邻域，$f(x_0)>f(x_0+\Delta x)$

$$f(x_0+\Delta x)-f(x_0)<0$$

左导数：

$$\lim_{\Delta x\to 0^{-}}{\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}}\ge 0$$

右导数：

$$\lim_{\Delta x\to 0^{+}}{\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}}\le 0$$

$f^{‘}{(x_0)}=0$ 驻点。

• 可导函数极值点是驻点。

• 驻点不一定是极值点。

• 极值点一定是驻点或导数不存在。

• 驻点导数不存在未必都是极值点。

定理：$f(x)$ 在 $(x_0-\delta,x_0+\delta)$ 内连续在邻域内，（$x_0$ 点可除外）可导。且 $f^{‘}{(x_0)}=0$ 或不存在。

• 左增右减极大值 $x\in (x_0-\delta,x_0)$，$f^{‘}{(x)}>0,x\in(x_0,x_0+\delta),f^{‘}{(x)}<0$

• 左减右增极小值 $x\in (x_0-\delta,x_0)$，$f^{‘}{(x)}<0,x\in(x_0,x_0+\delta),f^{‘}{(x)}>0$

• 左右都增（减），$x\in U(x_0)$，$f^{‘}{(x)}$ 不变号，不是极值。极值：

定义域：求导数 $=0$ 和不存在。

$f^{‘}{(x)}$ 左右符号：

左正右负，极大值

左负右正，极小值

左右同号，啥也不是

求函数数值

$$y=(x-1)^2(x+1)^3$$

定义域：$(-\infty,+\infty)$

$$y^{'}{(x)}=2(x-1)(x+1)^3+3(x-1)^2(x+1)^2$$ $$=(x-1)(x+1)^2(5x-1)$$ $$y^{'}=0,x=-1,\frac{1}{5},1$$

$x$	$(-\infty,-1)$	$-1$	$(-1,\frac{1}{5})$	$\frac{1}{5}$	$(\frac{1}{5},1)$	$1$	$(1,\infty)$
$f^{‘}$	$+$	$0$	$+$	$0$	$-$	$0$	$+$
$f$	增	非极值点	增	极大值点	减	极小值点	增

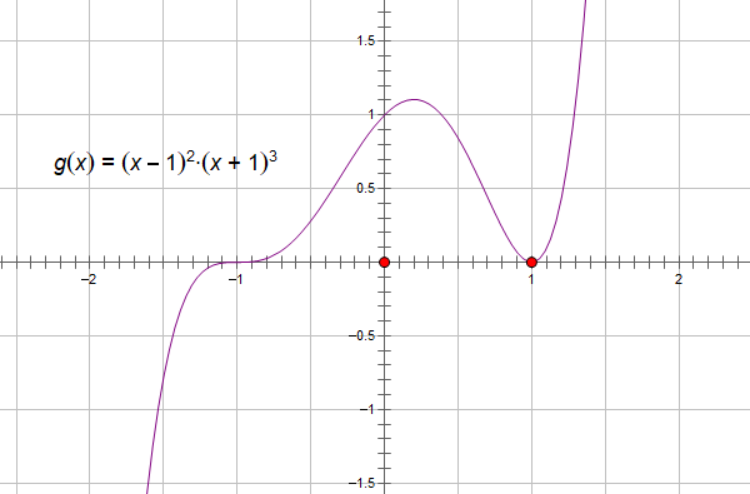
定理：$x_0$ 除，二阶导数。

$f^{‘}{(x_0)}=0,f^{‘’}{(x_0)}\not=0$

• $f^{‘’}{(x_0)}<0$ 极大值

$$f^{''}{(x_0)}=\lim_{x\to x_0}{\frac{f^{'}{(x)}-f^{'}{(x_0)}}{x-x_0}}=\lim_{x\to x_0}{\frac{f^{'}{(x)}}{x-x_0}}<0$$

$x_0$ 左，$x\in (x_0-\delta,x_0)$

$f^{‘}{(x)}>0,x_0$ 右，$x\in(x_0,x_0+\delta)$ $f^{‘}{(x)}<0$ 极大值。

• $f^{‘’}{(x_0)}>0$ 极小值

全局性，局部性

• 驻点

• 导数不存在

• 端点

$[a,b]$ 要检验 $f(a),f(b)$ 对最后结果是否有影响。

• 连续 $[a,b]$ 单调

• 区间内仅有一个极值，实际问题，区间内取，只有一个驻点。

函数作图

• 渐近线：水平渐近线，垂直渐近线，斜渐近线。

• 水平渐近线：

最大值接近渐近线：

$$\lim_{x\to +\infty}{f(x)}=b$$

最小值接近渐近线：

$$\lim_{x\to -\infty}{f(x)}=b$$

极值接近渐近线;

$$\lim_{x\to \infty}{f(x)}=b$$

$y=\frac{1}{x-1}$ 水平渐近线：

$$\lim_{x\to \infty}{\frac{1}{x-1}}=0$$

$y=0$ 水平渐近线。

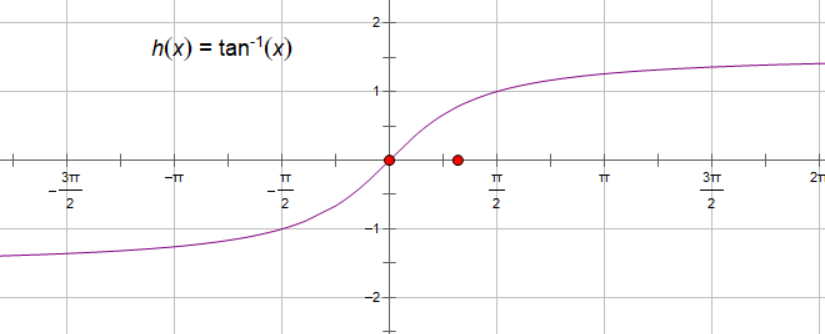
$y=\arctan x$ 渐近线;

$$\lim_{x\to +\infty}{\arctan x=\frac{\pi}{2}}$$ $$\lim_{x\to -\infty}{\arctan x=-\frac{\pi}{2}}$$

• 垂直渐近线：

$$\lim_{x\to c^{+}}{f(x)}=\infty$$ $$\lim_{x\to c^{-}}{f(x)}=\infty$$

$y=\frac{1}{1-x^2},x=-1,1$

$$\lim_{x\to 1}{\frac{1}{1-x^2}}=\infty$$ $$\lim_{x\to -1}{\frac{1}{1-x^2}}=\infty$$

$x=1,x=-1$ 垂直渐近线。

• 斜渐近线：

最大值逼近：

$$\lim_{x\to +\infty}{(f(x)-a_x)}=b$$ $$\lim_{x\to +\infty}{\frac{f(x)}{x}}=\lim_{x\to +\infty}{\frac{ax+b}{x}}=\lim_{x\to +\infty}{a+\frac{b}{x}}=a$$

最小值接近：

$$\lim_{x\to -\infty}{(f(x)-a_x)}=b$$ $$\lim_{x\to -\infty}{\frac{f(x)}{x}}=a$$

• 练习：

$f(x)\frac{x^3}{x^2+2x-3}$ 渐近线：

水平渐近线：

$$\lim_{x\to \infty}{\frac{x^3}{x^2+2x-3}}=\infty$$

（无水平渐近线）

垂直渐近线：

$$x^2+2x-3=0$$ $$x=-3,x=1$$ $$\lim_{x\to -3}{f(x)=\infty}$$ $$\lim_{x\to 1}{f(x)=\infty}$$

$x=-3,x=1$ 是垂直渐近线。

斜渐近线：

$$\lim_{x\to \infty}{\frac{f(x)}{x}}=\lim_{x\to \infty}{\frac{x^2}{x^2+2x-3}}=1$$ $$\lim_{x\to \infty}{(f(x)-x)=\lim_{x\to \infty}{\frac{x^3-x^3-2x^2+3x}{x^2+2x-3}}}=\lim_{x\to \infty}{\frac{-2x^2+3x}{x^2+2x-3}}=-2$$

（看最高次）

斜渐近线： $y=x-2$

微分法作图

• 定义域，不连续点，坐标轴相交

• 奇偶周期

• 渐近线，无穷远状态

• $f^{‘}{(x)}=0,f^{‘’}{(x)}=0$，$f^{‘},f^{‘’}$ 不存在的点，极值升降凹凸，拐点，特殊点。

• 练习：

$$y=e^{-x^2}$$

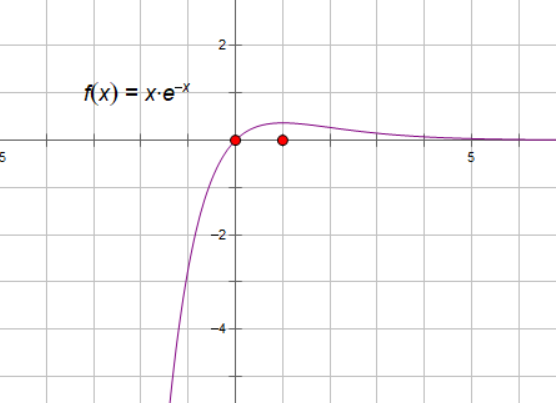
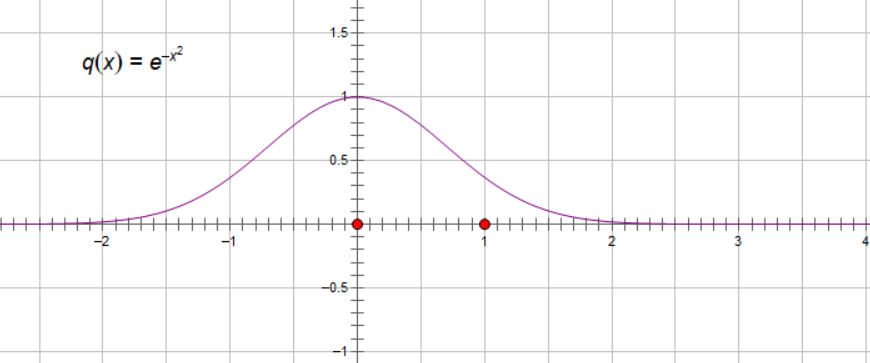
• 定义域：$(-\infty,+\infty),x=0,y=1,y>0,x$ 轴上方。

• 偶函数 $y$ 轴对称。

$$\lim_{x\to \infty}{\frac{1}{e^{x^2}}}=0$$

• $y=0$ 水平渐近线。

• $f^{‘}{(x)}=-2xe^{-x},f^{‘’}{(x)}=4{x^2-\frac{1}{2}}e^{-{x^2}}$

$x=0,f^{‘}{(x)}=0,x=\pm \frac{\sqrt{2}}{2},f^{‘’}{(x)}=0$

$x$	$(-\infty,-\frac{\sqrt{2}}{2})$	$-\frac{\sqrt{2}}{2}$	$(-\frac{\sqrt{2}}{2},0)$	$0$	$(0,\frac{\sqrt{2}}{2})$	$\frac{\sqrt{2}}{2}$	$(\frac{\sqrt{2}}{2},+\infty)$
$f^{‘}$	$+$	$+$	$+$	$0$	$-$	$-$	$-$
$f^{‘’}$	$+$	$0$	$-$	$-$	$-$	$0$	$+$
$f$	增，凹	拐点	增，凸	极大值	减，凸	拐点	减，凹

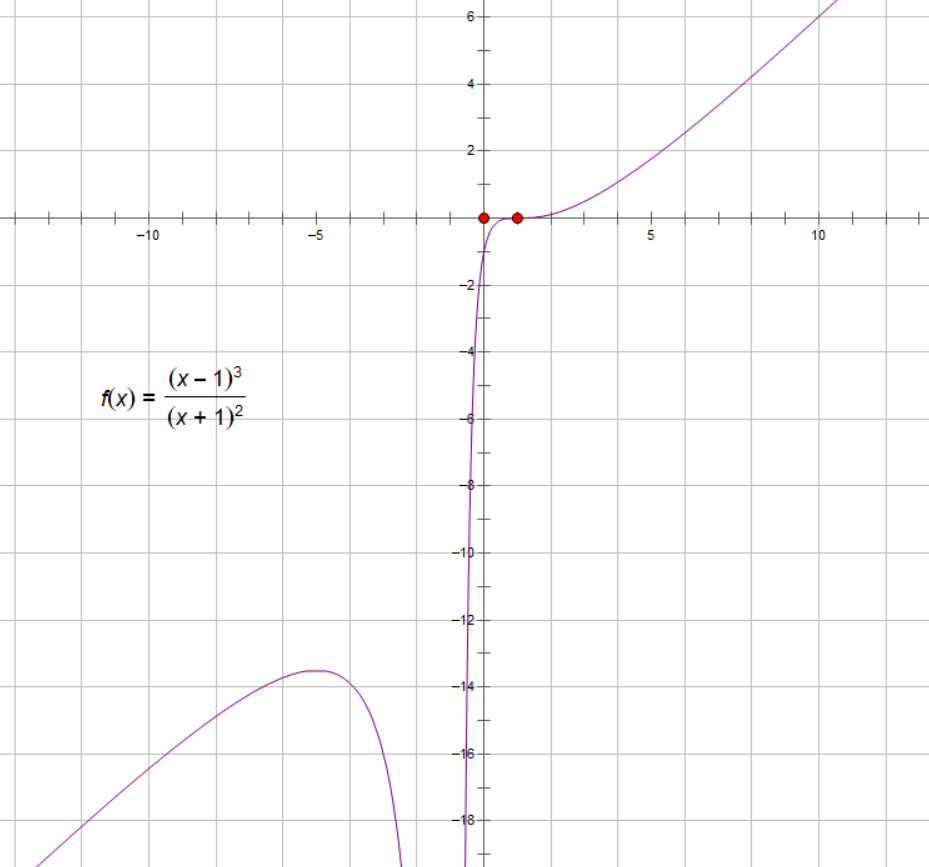
• 练习：

$$y=\frac{(x-1)^3}{(x+1)^2}$$

• $(-\infty,-1)\cup(-1,+\infty),x=-1$ 无穷间断点。$(-1,0),(0,1)$

• $x=-1$ 垂直。

$$\lim_{x\to \infty}{\frac{y}{x}}=\lim_{x\to \infty}{\frac{(x-1)^3}{x(x+1)^2}}=1$$ $$\lim_{x\to \infty}{\frac{y}{x}}=\lim_{x\to \infty}{(\frac{(x-1)^3}{(x+1)^2}-x)}=-5$$

斜渐近线：$y=x-5$。

$$y^{'}=\frac{(x-1)^2(x+5)}{(x+1)^3},y^{''}=\frac{24(x-1)}{(x+1)^4}$$

$x=-1,y^{‘},y^{‘’}$ 不存在。

$x$	$(-\infty,-5)$	$-5$	$(-5,-1)$	$-1$	$(-1,1)$	$1$	$(1,+\infty)$
$y^{‘}$	$+$	$0$	$-$	不存在	$+$	$0$	$+$
$y^{‘’}$	$-$	$-$	$-$	不存在	$-$	$0$	$+$
$y$	增，凸	极大值	减，凸	间断	增，凸	拐点	增，凹