定积分
- 概念
求曲边梯形面积
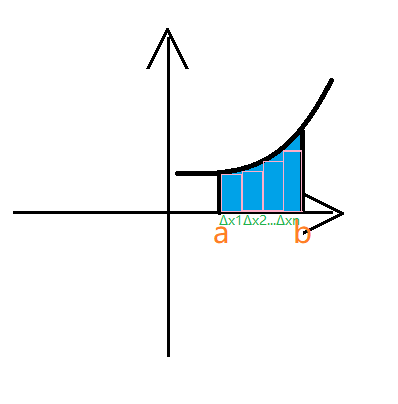
我们在 $(a,b)$ 找很多点 $a < x_1 < x_2 < x_3 < …, < x_n < b$ 再分别计算每段 $\Delta x_i$ 中找一个点 $\xi_i$ 对应的函数值。
- 定义:$f(x)$ 在 $[a,b]$ 有界,在 $[a,b]$ 上任意点插入分点,分成 $n$ 个小区间,$\Delta x_1,\Delta x_2,…,\Delta x_n$ 任取一点 $\xi_i$。
$a$ 积分下限,$b$ 积分上限,$x$ 积分变量。
注意:只与 $f(x)$ 与 $[a,b]$ 有关,与积分变量无关。
连续可积
有界,有限个断点可积
几何意义:
- $f(x)\ge 0$
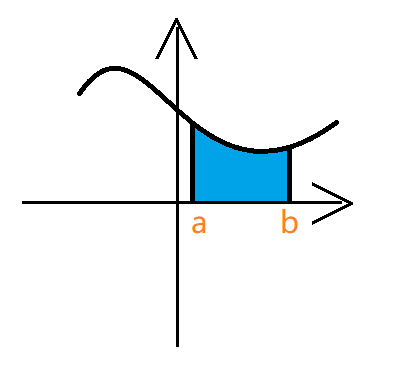
- $f(x)\le 0$
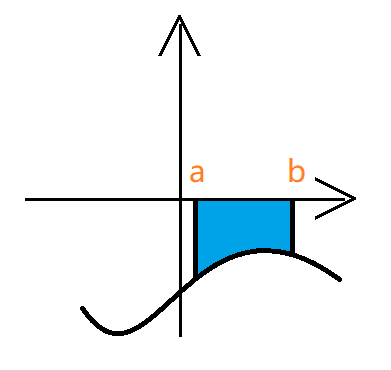
- $f(x)$ 有正有负
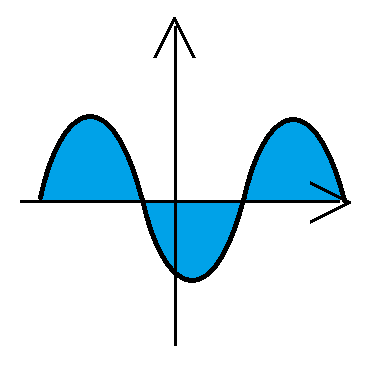
练习:
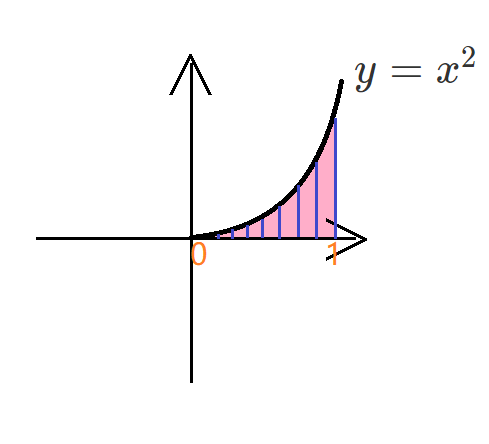
$[0,1]$ 登 $n$ 份,每份 $\frac{1}{n}$。
$\frac{\infty}{\infty}$ 洛必达法则:
逼近面积
- 矩形法

每份 $\Delta x=\frac{b-a}{n}$
- 梯形法:
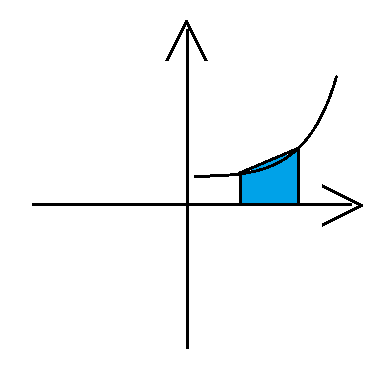
每个 $x_i$ 对应的函数值为 $y_i$。
- 抛物线:
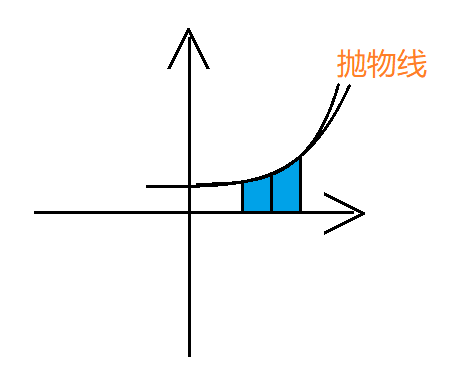
抛物线函数:$y=ax^2+bx+c$
所以三个点可以确定一个抛物线,假设找到了 $x_1,x_2,x_3$ 三个值,并求出 $y_1,y_2,y_3$,根据 $(x_1,y_1),(x_2,y_2),(x_3,y_3)$ 可以确定一个函数。
然后求出函数上三个点涵盖的下方的位置。
定积分性质
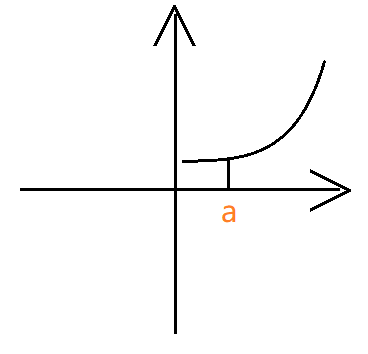
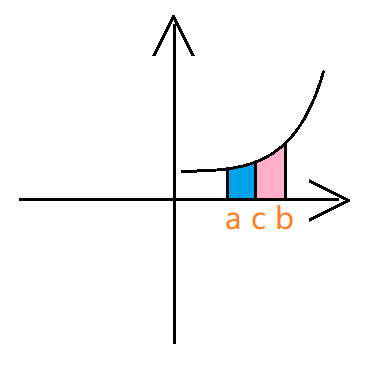
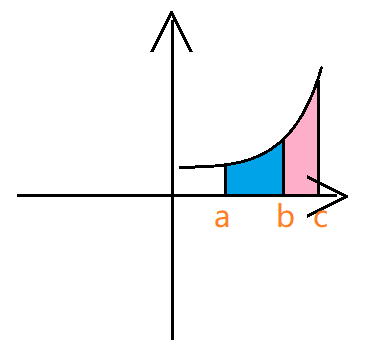
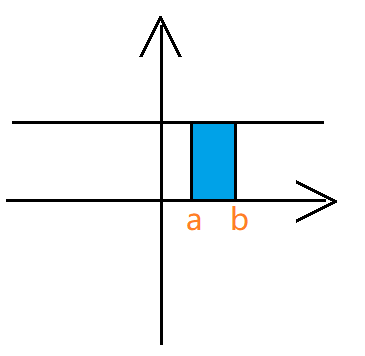
- 同号
推论:
- $M,m$ 为最大值,最小值,$m(b-a)\le\int^b_a{f(x)dx}\le M(b-a)$
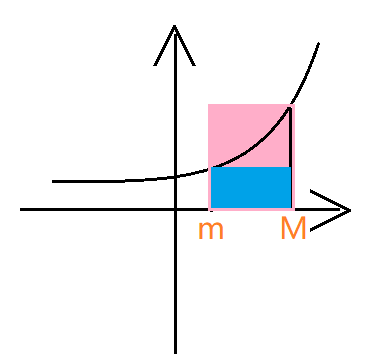
- 定积分的中值定理
$f(x)$ 连续,$\exists \xi \in[a,b]$
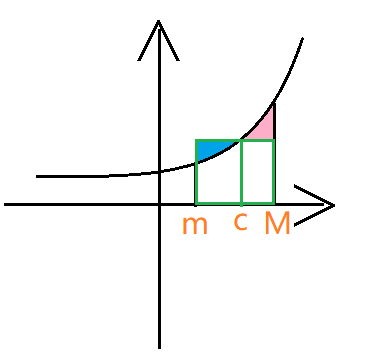
其中 $\frac{1}{b-a}\int^b_a{f(x)dx}$ 是一个数。
积分上限函数
其中 $x$ 变成自变量。
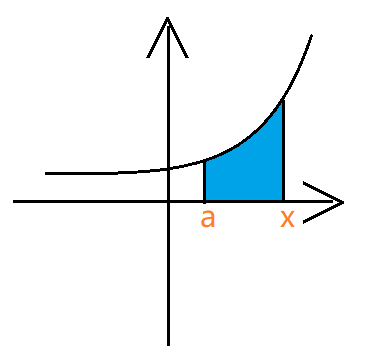
- 上限是 $x$,直接带入被积函数:
- 下限是 $x$,直接带入被积函数后前面加 $-$:
设 $k=x_2$
上限是 $g(x)$,首先将 $g(x)$ 带入被积函数,并计算 $g^{‘}{(x)}$。
下限是 $g(x)$,首先将 $g(x)$ 带入被积函数,并计算 $g^{‘}{(x)}$,最后前面加符号。
练习:
$\frac{0}{0}$ 洛必达法则
首先明白:
所以有:
$\frac{0}{0}$ 洛必达法则
无穷小替换可以快速出结果。
牛顿—莱布尼公式
实现定积分与不定积分的转换。
- 分类计算:
$P(x)=\int^x_0{f(t)dt}$ 在 $[0,2]$ 的值:
- $x\in [0,1]$
- $x\in (1,2]$
带入计算即可。
换元积分方法
$g(t)$ 单调递减(增)
上下限改变,原变量上限对新变量上限,原变量下限对新变量下限。
换元时,上下限跟着换。
练习:
设 $t=\sqrt[3]{x},t^3=x,dx=3t^2dt$。
$x$ 从 $0$ 到 $8$,$t$ 从 $0$ 到 $2$。
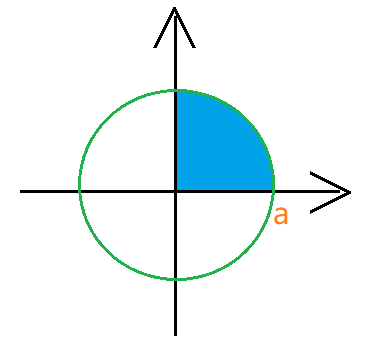
$x$ 从 $0$ 到 $a$,$t$ 从 $0$ 到 $\frac{\pi}{2}$。
函数奇偶性影响
- $f(x)$ 偶:
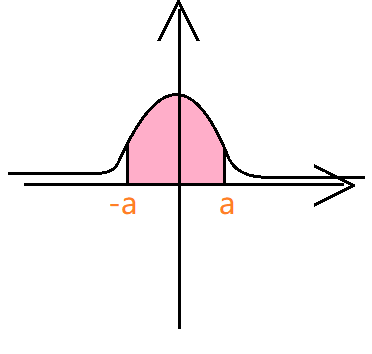
- $f(x)$ 奇:
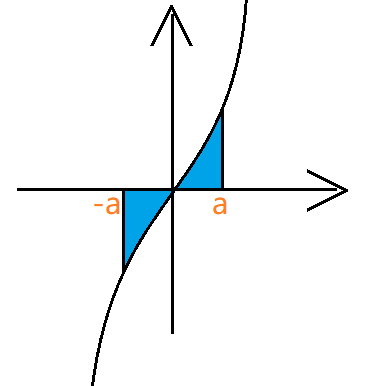
- 练习:
$\sin^3 x$ 奇函数,$1+x^2$ 偶函数,$\frac{\sin^3 x}{1+x^2}$ 奇函数,根据它的范围所以:
$(\arctan x)^2$ 偶函数,$1+x^2$ 偶函数,$\frac{(\arctan x)^2}{1+x^2}$ 偶函数,根据它的范围所以:
- 证明:
令 $x=\frac{\pi}{2}-t,dx=-dt$
$x$ 从 $0$ 到 $\frac{\pi}{2}$,$t$ 从 $\frac{\pi}{2}$ 到 $0$。
部分积分法
不定积分:
定积分:
- 将里面的提到 $d$ 后面一般的顺序(优先级):
- 练习:
$x-2=t$,$x$ 从 $1$ 到 $4$,$t$ 从 $-1$ 到 $2$,$dx=dt$
积分实际用例
求面积
- 两函数夹的面积
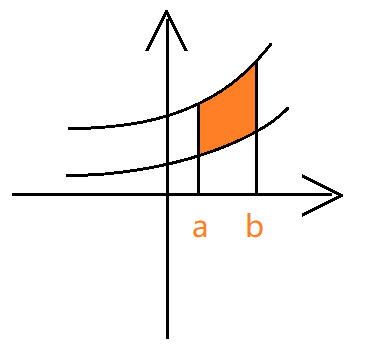
上面的是 $y=f(x)$,下面的是 $y=g(x)$ 用上面的值减下面的值,求得面积,由于面积 $> 0$ 所以要注意是上面减下面。
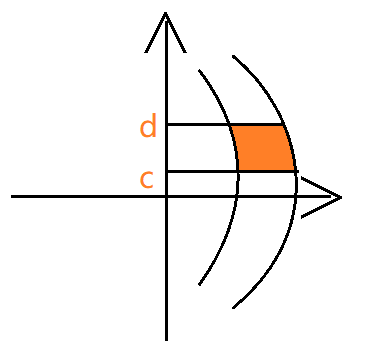
左面的是 $x=g(y)$,右面的是 $x=h(y)$ 用右面的值减左面的值,求得面积,由于面积 $> 0$ 所以要注意是右面减左面。注意这时最好将表达式转换成用 $y$ 描述 $x$。
- 练习:
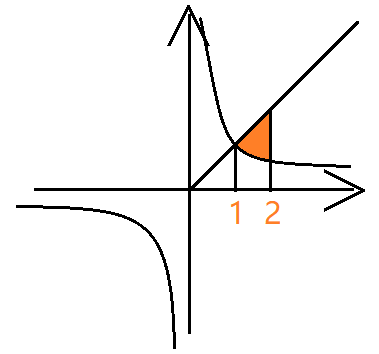
画图
判断垂直于哪个轴
保证,上 $-$ 下,右 $-$ 左(分区间讨论)。
练习:
求 $y\in[-2,4]$ 中 $y=x-4$ 和 $y^2=2x$ 围成的面积。
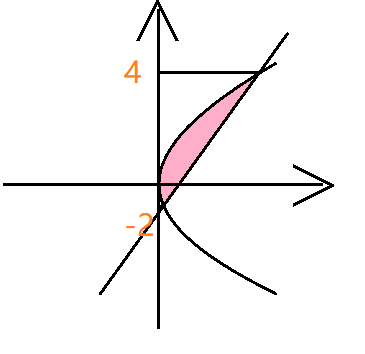
改写表达式:
求体积
$A(x)$ 代表的是当前 $x$ 值对应的横截面积。
- 绕x轴旋转
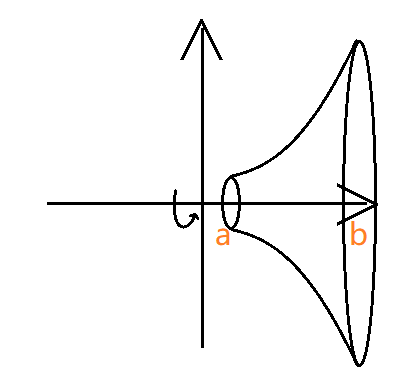
- 绕y轴旋转
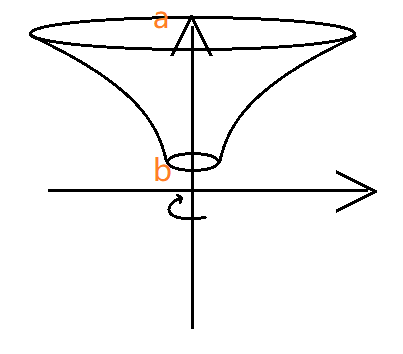
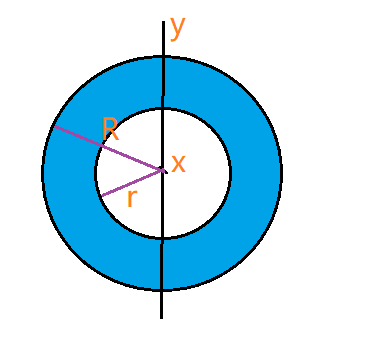
求 $x+y=4$ 和 $xy=3$ 围成的图形绕 $x$ 轴旋转形成的体积。
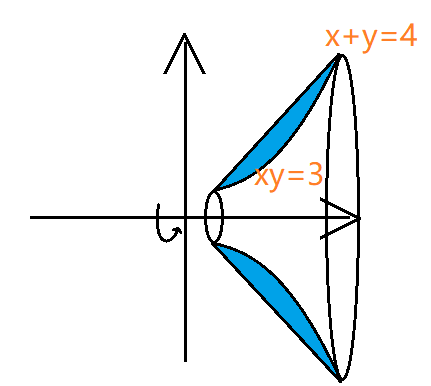
截面图:
经济问题
- 边际函数 $\rightarrow$ 原函数
总产量变化率 $f(t)=100+12t-0.6t^2$ 求,$t=2$ 到 $t=4$ 的产量。
$P(t)$ 是产量。
- 取钱
年利率 $r$。
$P(0)$ 现在的钱,$P(t)$ 以后的钱。
一年结 $n$ 次,每次利率 $\frac{r}{n}$,$t$ 年结 $nt$ 次。
- 投资收益
$R(t)$ 每年的收益,$R$ 总收益。
如果 $R(t)$ 是常数:
练习:
$50$ 万投资 $10$ 年,每次分得 $4\%$,每年收益多少钱?
$50=A\int_0^10{e^{-0.04t}dt}$
$A=6.066$ 万元。
广义积分
- 无限积分
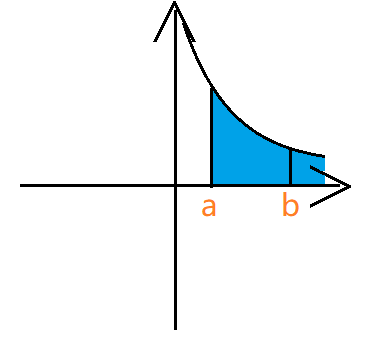
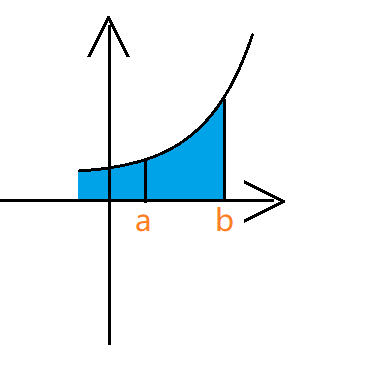
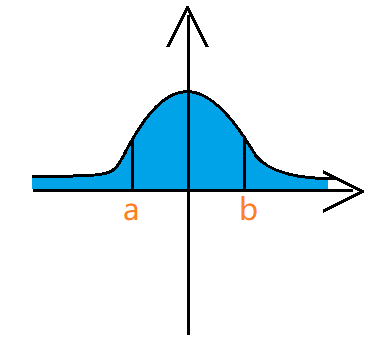
分别用 $1,2$ 的情况处理即可。
练习:
广义牛顿-莱布尼公式
- 练习:
发散,收敛
发散。
- 练习:
- 常数:
收敛。那么:
收敛。
- 函数之间加减
收敛。那么:
收敛。
收敛判定
- 定理:$f(x\ge 0)$
$\int^{+\infty}_a{f(x)dx}$ 收敛 $\Leftrightarrow$ $p(x)\int^{x}_a{f(t)dt}$ 有界
定理比较:$0\le f(x)\le g(x)$
收敛,那么:
是收敛。
发散,那么:
发散。
- 练习:
收敛。
条件收敛,绝对收敛
如果:
收敛,
收敛,那么:
绝对收敛。如果:
收敛,
发散,那么:
条件收敛。
$\int^{+\infty}_a{|f(x)|dx}$ 收敛 $\Rightarrow \int^{+\infty}_a{f(x)dx}$ 收敛。
瑕积分
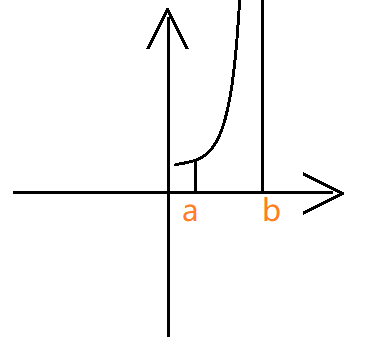
在 $b$ 上没有定义。那么就让 $b$ 向左亿点点($-\xi^{+}$)
同样:
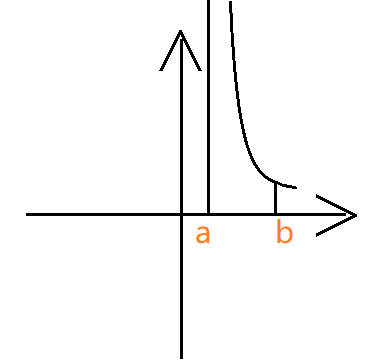
$a$ 没有定义:
中间未定义:
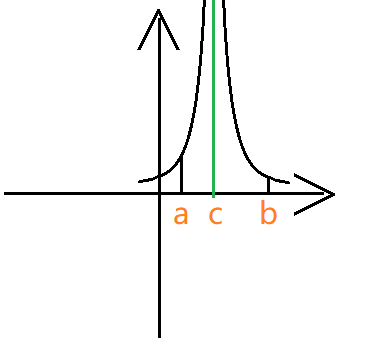
带入情况 $1,2$ 即可。
练习:
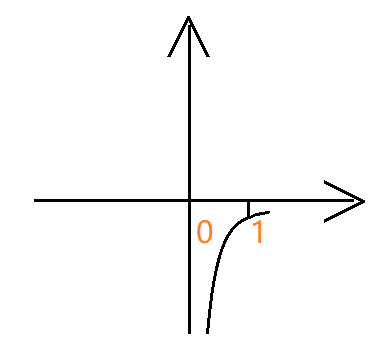
- 中间没有定义:
$\Gamma$ 函数
- 练习:

