最小树形图
其实就是有向的 最小生成树。
从根节点,可以到达所有节点,那么可以形成很多树,走过的路径综合最小的就是最小树形图(有向图)。如果一条路都没有,就不能找出树形图,输出 $-1$。
不难发现,有很多种情况出现的原因是“环”的存在,所以要找最小树形图,就要不断找“环”,求出环的最优情况。不断缩点,就可以找到最小值了。(思想类似于发问题分成小问题,解决小问题就解决了问题)。
注意:根节点是不能被指向的,因为那一定不优!
朱刘算法
从小到大统计所有节点的理论最小值(别的点到达这一点的最小值)。同时根据统计的来的节点判断处理是否会形成环,如果形成环,缩点处理(贪心的处理,其实就是暴力找最小环)。
在所完后的时候,所有指向新点的边都要减去环中的最小边的值(类似于反悔贪心的思想)。
代码实现思路
读入基本信息。
初始化基本信息。
记录到大每个点的最小权值(理论最小值)和从何来的点。
如果发现有断点(不能成树)直接返回 $-1$。
找到新环,统计权值(同时缩点)。
更新和新点有关的边。
继续找是否还有环。
更新点的数量(缩好的环上的点,全被“屏蔽”了)。
输出结果。
代码
#include<iostream>
#include<cstring>
#include<string>
#include<cstdio>
#include<algorithm>
#include<cctype>
using namespace std;
int r_r(){//快读
int x=0,f=1;
char c=getchar();
while(!isdigit(c)){
if(c=='-')f=-1;
c=getchar();
}
while(isdigit(c)){
x=(x<<1)+(x<<3)+(c^48);
c=getchar();
}
return x*f;
}
const int o_o=1e6+10;
const int m_a=1e9+10;
int n,m;
int g_g;//根节点
long long a_s;
struct po{
int u;//从而来的点
int v;//去往的点
int w;//权值
}p_p[o_o];
int x_p;//当前图环的数量
int i_d[o_o];//每个点的新节点编号
int t_p[o_o];//链头
int f_a[o_o];//到当前节点最小值的路径是由哪个点提供的
int m_i[o_o];//到当前节点的理论最小值
int g_a(){
while(1){
for(int i=1;i<=n;++i){//初始化
i_d[i]=t_p[i]=0;
m_i[i]=m_a;
}
for(int i=1;i<=m;++i)//遍历每条边
if(p_p[i].u!=p_p[i].v&&p_p[i].w<m_i[p_p[i].v]){//不是自环并且到其他节点的值更优
f_a[p_p[i].v]=p_p[i].u;//更新来的路径节点
m_i[p_p[i].v]=p_p[i].w;//更新最小值
}
int k_k=m_i[g_g]=0;//初始化根节点
for(int i=1;i<=n;++i){//枚举节点
if(m_i[i]==m_a)return 0;//不连通
a_s+=m_i[i];//统计所有点的理论最小值
for(k_k=i;k_k!=g_g&&t_p[k_k]!=i&&!i_d[k_k];k_k=f_a[k_k])//非链顶节点向上爬,不在环中
t_p[k_k]=i;//更新链顶
if(k_k!=g_g&&!i_d[k_k]){//不是根节点并且不在环中
i_d[k_k]=++x_p;//开新点(缩点)
for(int j=f_a[k_k];j!=k_k;j=f_a[j])i_d[j]=x_p;//更新环上的节点的新节点
}
}
if(!x_p)return 1;//没有点了
for(int i=1;i<=n;++i)if(!i_d[i])i_d[i]=++x_p;//节点没有在环内的,自己开新点
for(int i=1;i<=m;++i){//枚举所有边
int l_t=m_i[p_p[i].v];//记录当前边通向的节点的理论最小值
if((p_p[i].u=i_d[p_p[i].u])!=(p_p[i].v=i_d[p_p[i].v]))p_p[i].w-=l_t;//不在一个环中更新边的价值
}
n=x_p;//更新点的数量
g_g=i_d[g_g];//更新根节点
x_p=0;//初始化环编号
}
}
int main(){
n=r_r();m=r_r();g_g=r_r();
for(int i=1;i<=m;i++){//读入存边
p_p[i].u=r_r();
p_p[i].v=r_r();
p_p[i].w=r_r();
}
if(g_a())printf("%lld",a_s);//输出结果
else puts("-1");
return 0;
}左偏树优化
为了快速找到最小入边。
左偏树
外节点:有叶子结点是空。
距离:$d$ (代码中所谓的“深度”),树上结点到最近的外节点的距离。
堆性质:父节点的价值比儿子小。
左偏:左子叶的深度不比右子叶深度小(距离短)。
注意:$d_x=d_r+1$(节点的深度一般是右子叶的深度 $+1$)
那么根据题目的要求,我们需要写出:合并堆,删点,并查集。
代码思路
初始化信息。
处理合并堆。
先判断是否存在子叶,然后保证“左偏”,继续向下处理(右子树和当前右树(同辈)比较更新),最后更新“深度”。
处理删点。
判断是否存在,将目标点删掉。更新子树父节点,合并子树。
左偏树代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
using namespace std;
int r_r(){//快读
int x=0,f=1;
char c=getchar();
while(!isdigit(c)){
if(c=='-')f=-1;
c=getchar();
}
while(isdigit(c)){
x=(x<<1)+(x<<3)+(c^48);
c=getchar();
}
return x*f;
}
const int o_o=1e6+10;
struct po{
int d;//节点深度
int f_a;//父节点
int v;//编号
int s_n[2];//子节点
}t_r[o_o];
int f(int k){//找父节点
if(t_r[k].f_a==k)return k;
return t_r[k].f_a=f(t_r[k].f_a);
}
int b_g(int l,int r){//合并堆
if(!l||!r)return l+r;//存在至少其中一个子树是空子树
if(t_r[l].v>t_r[r].v||(t_r[l].v==t_r[r].v&&l>r))swap(l,r);
//保证左子树编号小于右子树编号
t_r[l].s_n[1]=b_g(t_r[l].s_n[1],r);//继续合并右子树,并存根节点
if(t_r[t_r[l].s_n[0]].d<t_r[t_r[l].s_n[1]].d)swap(t_r[l].s_n[0],t_r[l].s_n[1]);
//保证左子树的深度不小于右子树深度
t_r[t_r[l].s_n[0]].f_a=t_r[t_r[l].s_n[1]].f_a=t_r[l].f_a=l;
//更新左右子树和当前节点父节点
t_r[l].d=t_r[t_r[l].s_n[1]].d+1;//更新深度
return l;//返回根节点编号
}
void d_l(int k){//删点
t_r[k].v=-1;//更新标记(已经被删了)
//更新左右子树的父节点,变回它们本身
t_r[t_r[k].s_n[0]].f_a=t_r[k].s_n[0];
t_r[t_r[k].s_n[1]].f_a=t_r[k].s_n[1];
//合并左右子树
t_r[k].f_a=b_g(t_r[k].s_n[0],t_r[k].s_n[1]);
}
int main(){
int n=r_r(),t=r_r();
t_r[0].v=-1;//初始化根节点标记
for(int i=1;i<=n;i++){
t_r[i].f_a=i;//初始化父节点
t_r[i].v=r_r();//读入权值
}
while(t--){
int op=r_r(),x=r_r();
if(op==1){//合并堆
int y=r_r();
if(t_r[x].v==-1||t_r[y].v==-1)continue;//存在点已经被删了
//找堆的父节点(根)
int f_1=f(x);
int f_2=f(y);
//不在同一个堆中,要合并堆
if(f_1!=f_2)t_r[f_1].f_a=t_r[f_2].f_a=b_g(f_1,f_2);
}else {//删除最小值
if(t_r[x].v==-1)puts("-1");//堆空
else {
printf("%lld\n",t_r[f(x)].v);//输出最小值
d_l(f(x));//删点
}
}
}
return 0;
}优化的代码思路
主要思路(这里的图为了描述边是按照从小到大得权值判断的,画的过程有些夸张,实际上,会直接找到第一小的环处理):
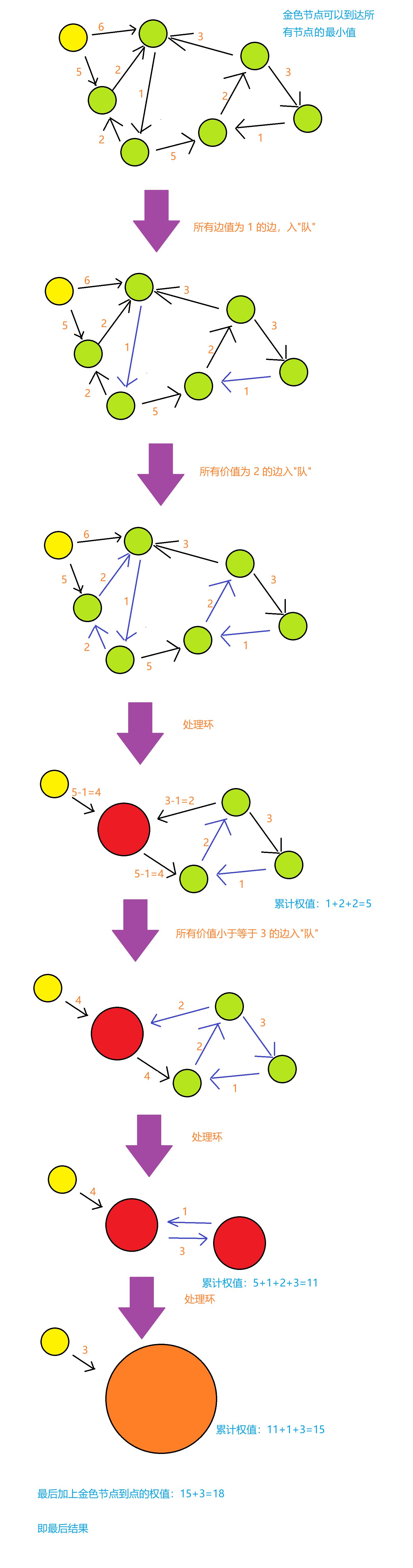
同样是反悔贪心的思想。
读入信息并初始化所有信息。
度读入时,将所有可以到当前点的点和权值存入以当前节点为根的左偏树中。(主要优化取点)。
这样根据边权值找新环,缩点,统计。
更新和新点有关的边的权值。
当所有点都处理后,输出结果即可。
优化后代码
没有指针!
#include<iostream>
#include<cstring>
#include<string>
#include<cstdio>
#include<algorithm>
#include<cctype>
using namespace std;
int r_r(){//快读
int x=0,f=1;
char c=getchar();
while(!isdigit(c)){
if(c=='-')f=-1;
c=getchar();
}
while(isdigit(c)){
x=(x<<1)+(x<<3)+(c^48);
c=getchar();
}
return x*f;
}
const int o_o=1e5+10;
int f_a[o_o];//存父节点
int x_p;//开新点的编号
int b_b[o_o];//点是否被遍历过
struct po{
int l,r;//左右子树
int d;//深度
int v_l;//边权
int l_n;//懒标记,到点的最小值。所有相关的边都要减。
int u;//从哪个点来的
po(){//初始化
int l=0,r=0;
int d=-1;
int v=0;
int l_n=0;
int u=0;
}
}t_r[o_o];
int g_g[o_o];//每个点多可以成为临时根节点(环的“根”)
void b_g(int&x,int&y){//小根堆合并
if(!x||!y){//有一个树是空
x^=y;//直接更新
return;
}
if(t_r[x].v_l>t_r[y].v_l)swap(x,y);//保证主树干“粗”
t_r[y].l_n-=t_r[x].l_n;//更新懒标记
t_r[y].v_l+=t_r[x].l_n;//更新权值
b_g(t_r[x].r,y);//继续合并右子树
if(t_r[t_r[x].l].d<t_r[t_r[x].r].d)swap(t_r[x].l,t_r[x].r);//保证左子树深度大
t_r[x].d=t_r[t_r[x].r].d+1;//深度更新
}
int f(int x){//找父节点
if(f_a[x]==x)return x;
return f_a[x]=f(f_a[x]);
}
void g_f(int u,int v){
if((u=f(u))!=(v=f(v))){//是否公共祖先
b_g(g_g[v],g_g[u]);//合并小根堆
f_a[u]=v;//公共祖先
}
}
void p_d(int&k){//懒标记下传
t_r[t_r[k].l].l_n+=t_r[k].l_n;
t_r[t_r[k].r].l_n+=t_r[k].l_n;
//更新边权
t_r[t_r[k].l].v_l-=t_r[k].l_n;
t_r[t_r[k].r].v_l-=t_r[k].l_n;
t_r[k].l_n=0;//清空标记
}
void x_y(int&x){//将右子树并到左子树中
p_d(x);//释放懒标记
b_g(t_r[x].l,t_r[x].r);//将右子树并到左子树中
x=t_r[x].l;//更新根节点
}
int t_p(int&x){
while(g_g[x]&&f(t_r[g_g[x]].u)==x)x_y(g_g[x]);//将右子树并到左子树中
if(!g_g[x]){//不存在根节点
puts("-1");//图不连通
exit(0);//结束运行
}
t_r[g_g[x]].u=f(t_r[g_g[x]].u);
//更新来的点(直接更新记录“根节点”即可)已经将环缩成点了
return g_g[x];//返回根节点序号
}
int i_n[o_o];//到当前点的点
int main(){
int n=r_r(),m=r_r(),r=r_r();//读入
int a_s=0;//初始化
x_p=n;//初始化点的个数
b_b[r]=r;//标记
for(int i=1;i<=m;++i){
int u=r_r(),v=r_r(),w=r_r();//读入
t_r[i].v_l=w;//记录价值
t_r[i].u=u;//记录来点
t_r[i].d=0;//更新深度
int k_k=i;//临时标记(防止合并时更新 i 的值,导致无限循环)
b_g(g_g[v],k_k);//当前节点加入到目标小根堆中
}
int k_k;//临时变量,存根节点编号
for(int i=1;i<=n<<1;++i)f_a[i]=i;//初始化父节点
for(int i=1,j=i;i<=n;j=++i)//枚举节点
while(!b_b[j]){//点未遍历过
while(!b_b[j]){//点未遍历过
b_b[j]=i;//标记
k_k=t_p(j);//记录根节点编号
j=t_r[k_k].u;//爬向来的节点(往回爬)
a_s+=t_r[k_k].v_l;//统计权值
}
if(b_b[j]!=i)break;//不是同一个环了,结束
while(b_b[j]>=0){
b_b[j]=-1;//标记
k_k=t_p(j);//记录根节点编号
j=i_n[j]=t_r[k_k].u;//往回爬并记录
t_r[k_k].l_n+=t_r[k_k].v_l;
//更新懒标记,边的理论最小值(懒标记更新为负数)
//代表每个相关联的边要减去的量
t_r[k_k].v_l=0;//更新边的价值
}
++x_p;//开新点(缩环后的点)
while(b_b[j]==-1){//恢复标记,善后
b_b[j]=i;//更新环标记
g_f(j,x_p);//新节点连入树中,在树上建立“坐标”
j=i_n[j];//上爬
}
j=x_p;//下回更新新点
}
printf("%d",a_s);//输出结果
return 0;
}
