前置思想:manacher
回文自动机
题目让我们求以每个字符结尾的回文串有多少个(注意给的原串需要解密)。
manachar 算法将回文的边界提出缩短了使得效率比暴力要高,但是并没有实现串与串之间的关系连接。而实现串之间的关系,就会想到要用 trie 树,然后通过字符串之间的关系配置失配指针,然后形成 trie 图或者说自动机来解决问题。
那么如何建立回文的自动机?
首先我们知道回文串分为两种:长度为奇,长度为偶。(按长度区分,长度为奇的回文串的回文中心是一个字符,而长度为偶的字符串回文中心是两个字符之间的位置。)
那么了解这个性质后,我们有了两棵树:
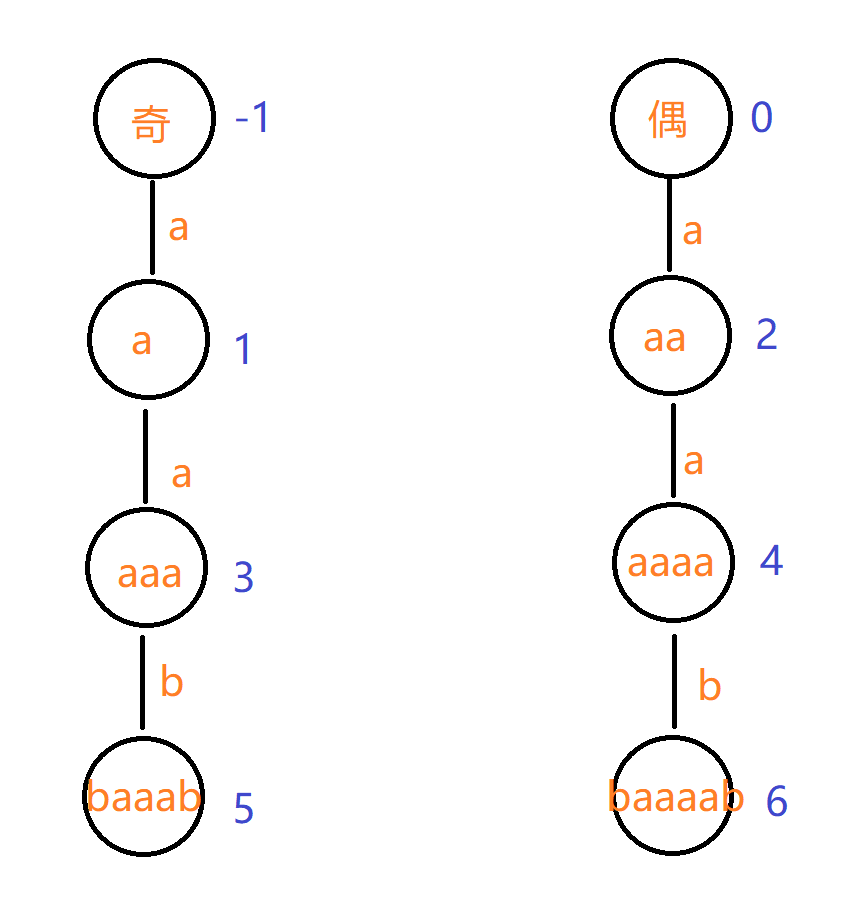
(这里为了方便理解没有增加更多的枝干)
首先有两个根区分了奇偶串,并在长度旁边标注了字符串的长度。(注意:奇根的长度是 $-1$,这是为了名在后面合并的时候,可以直接和偶根树合并到,长度可以直接增加相同的 $2$,而不是再分类讨论。)
这时枝干的字符为两边增加的字符(相当于给回文串劈开讨论)。奇偶根树路径合并(路径相同的串)。
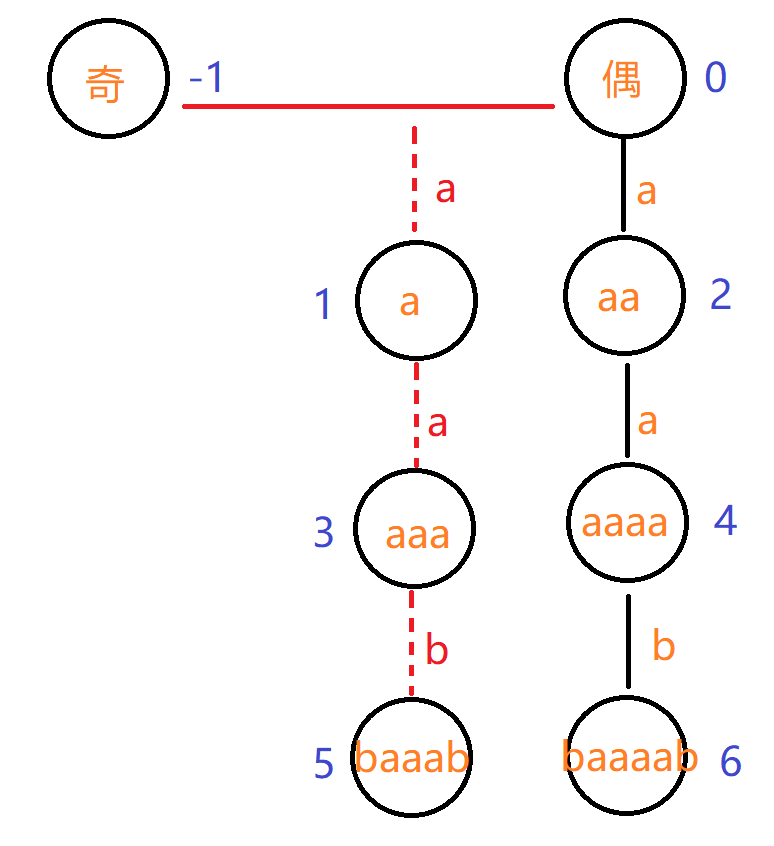
红色虚线是说明虽然在一条枝干上,但是奇偶串的奇偶性并没有变,由于我们的奇根设置的是 $-1$ 所以可以直接接上。(其实这里的合并并不是真的合并,只为了更方便理解失配指针)。
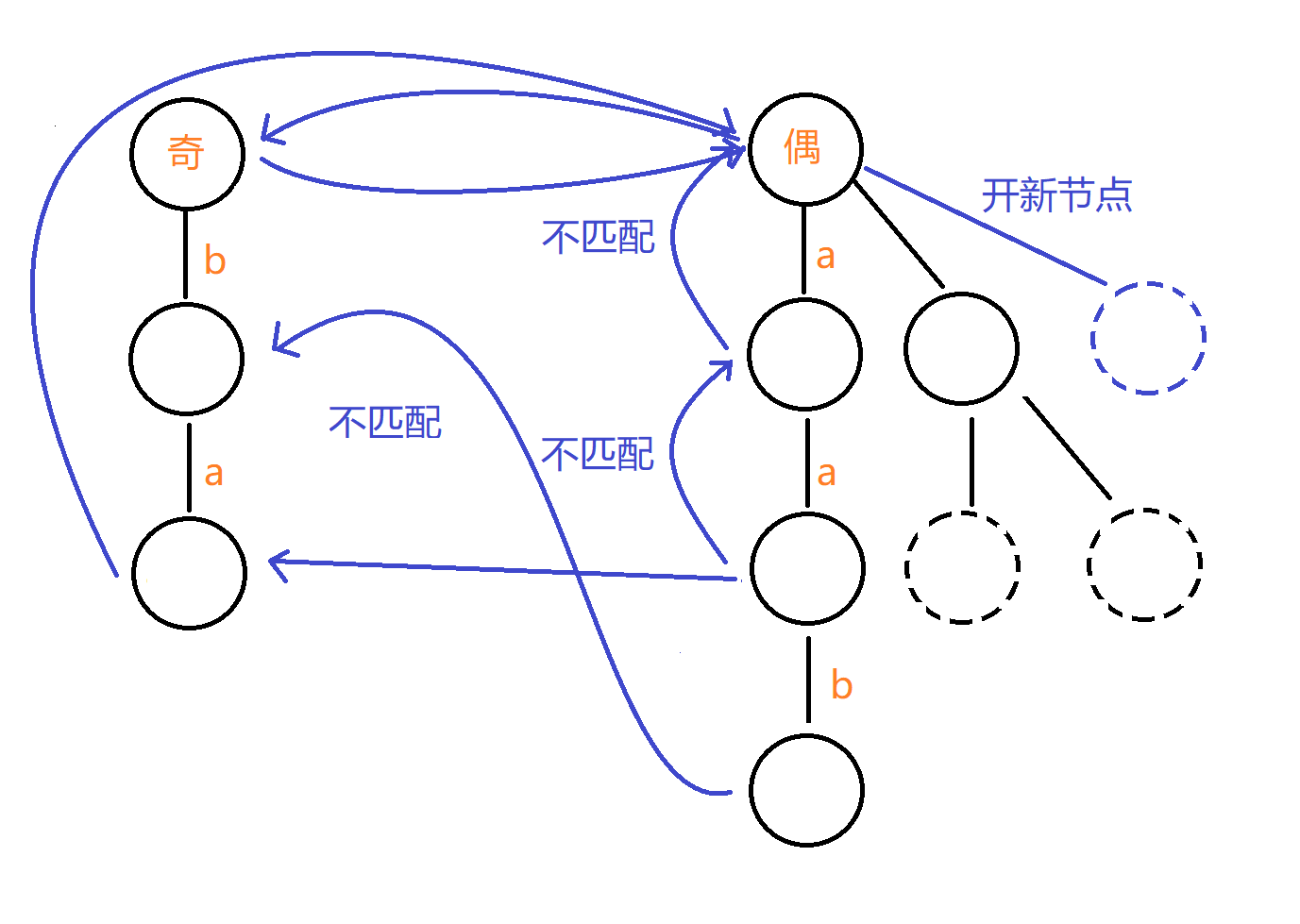
(有些失配指针没画全,只挑几个有代表性的画了,方便理解)。
但是其中的性质其实并不难:应为我们要找的是当前位置的字符结尾的回文串,那么一定知道,结尾的字符是不变的,所以我们只要找到失配指针指向的结尾字符相同的地方才会匹配成功,其他字符就不用考虑了。失配指针就是每回找到已经匹配成功的字符串中结尾(或者说开头)和当前字符相同的回文串,进行比对,这样一旦匹配不成功,也是直接跳到记录的地方再进行比配,如果实在没有匹配成功或者没有记录,就会开新节点记录以备下次的使用。
代码
#include<iostream>
#include<cstring>
#include<string>
#include<cstdio>
#include<algorithm>
#include<cctype>
#include<queue>
using namespace std;
int r_r(){//快读
int x=0,f=1;
char c=getchar();
while(!isdigit(c)){
if(c=='-')f=-1;
c=getchar();
}
while(isdigit(c)){
x=(x<<1)+(x<<3)+(c^48);
c=getchar();
}
return x*f;
}
const int o_o=2e6+10;
int n;//字符长度
char s[o_o];//原串
int l_n[o_o];//该节点表示的已经匹配成功的回文字符串长度
int s_m[o_o];//x 节点每个回文串出现次数(即统计的答案)
int f_l[o_o];//失配指针
int m_l;//失配指针中能匹配到的最长回文后缀
int k_k;//记录中找到的最长回文后缀的点的标号
int t_r[o_o][26];//记录儿子节点
int x_p=1;//节点数(用来建新节点)
int g_f(int x,int i){//处理失配指针
while(i-l_n[x]-1<0||s[i-l_n[x]-1]!=s[i])x=f_l[x];
//比较串头和当前字符比较
//往回跳,找到能匹配的位置
return x;//返回找到的编号
}
int main(){
scanf("%s",s);//读入子串
n=strlen(s);//计算长度
f_l[0]=1;//初始化失配指针
l_n[1]=-1;//初始化奇节点的值
for(int i=0;i<=n-1;i++){
if(i>=1)s[i]=(s[i]+s_m[m_l]-97)%26+97;//解密码
//找到 m_l 的失配指针中能匹配到的最长回文后缀
k_k=g_f(m_l,i);
if(!t_r[k_k][s[i]-'a']){//没有建过点,建点
f_l[++x_p]=t_r[g_f(f_l[k_k],i)][s[i]-'a'];
//记录上次能匹配成功的地方,失配了直接过去
//建新节点更新失配指针
t_r[k_k][s[i]-'a']=x_p;//接儿子
l_n[x_p]=l_n[k_k]+2;//更新长度(每回左右同时扩展,长度增加 2)
s_m[x_p]=s_m[f_l[x_p]]+1;//更新结果(回文串的个数)
}
m_l=t_r[k_k][s[i]-'a'];//建过点,直接用
printf("%d ",s_m[m_l]);//输出
}
return 0;
}
