集
支配集
- 支配集
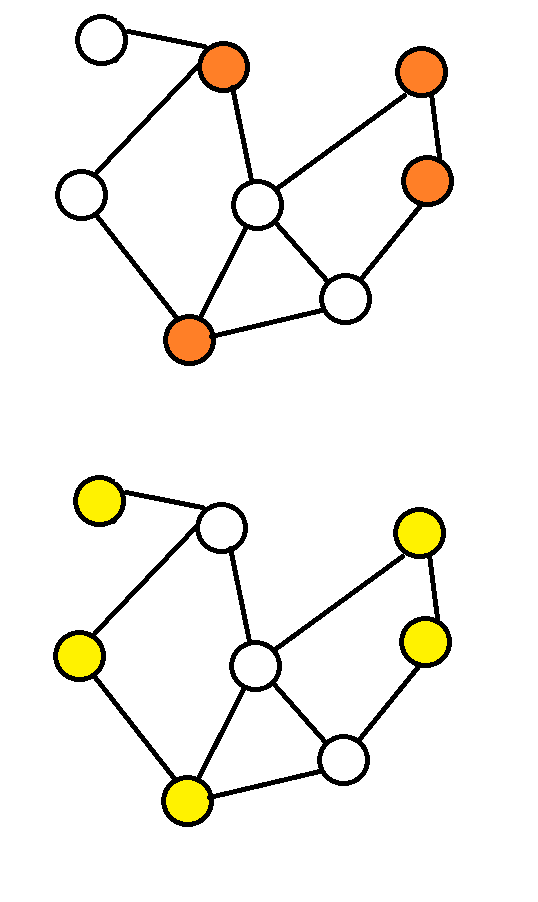
定义:所有的点都和点集(支配集)中的点直接相连(有边相连)。
- 极小支配集
定义:点集中去掉任意一个点就不是支配集。
- 最小支配集
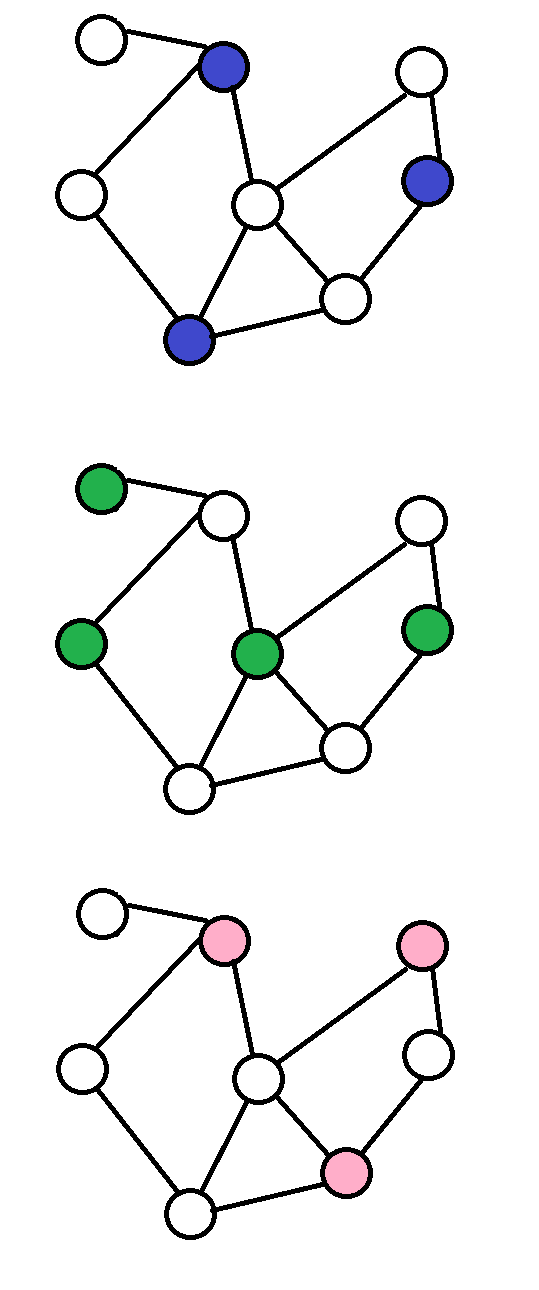
定义:极小支配集中用的点数最少的点集(上图中第 $1,3$ 个都是)。
最小支配集一定是极小支配集。
极小支配集不一定是最小支配集。
独立集
- 独立集
定义:点集中不存在两点之间有直接连边。
- 极大独立集
定义:图上的所有的不在点集中的点,任意一个点加入点集,不再是独立集。
- 最大独立集
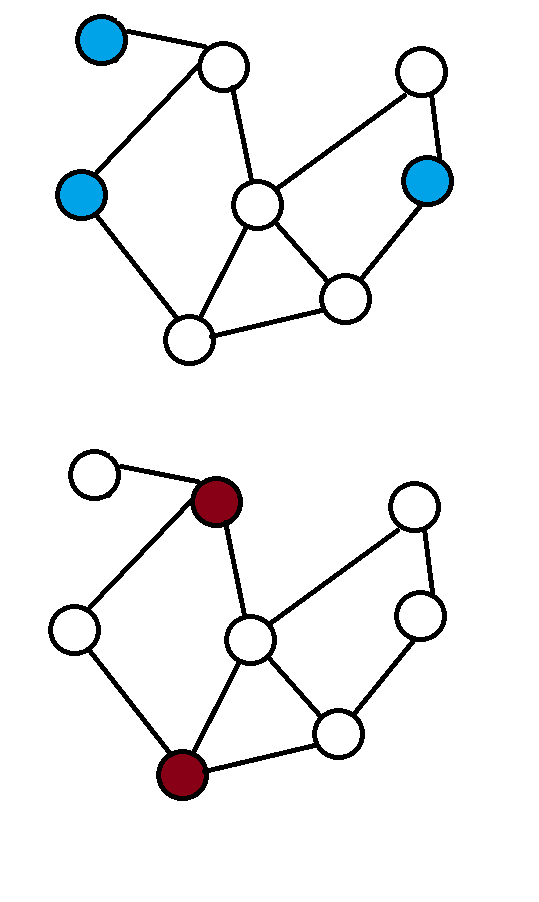
定义:极大独立集中,点数最多的独立集。
覆盖集
- 覆盖集
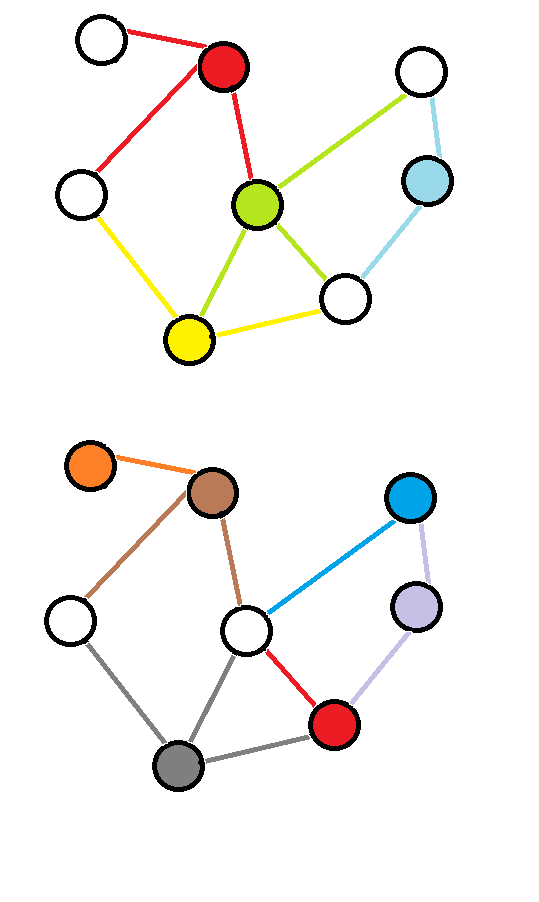
定义:图上所有的边的至少一个端点在点集中。
- 最小覆盖集
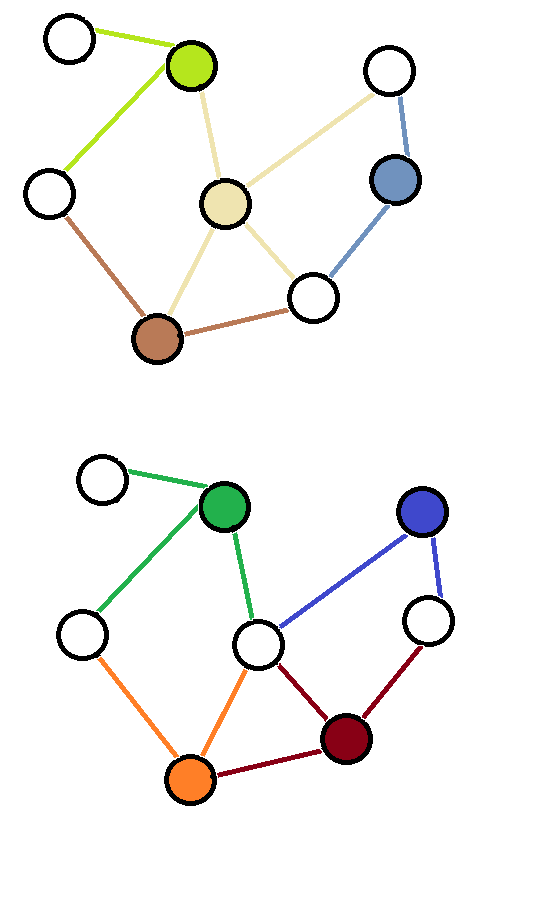
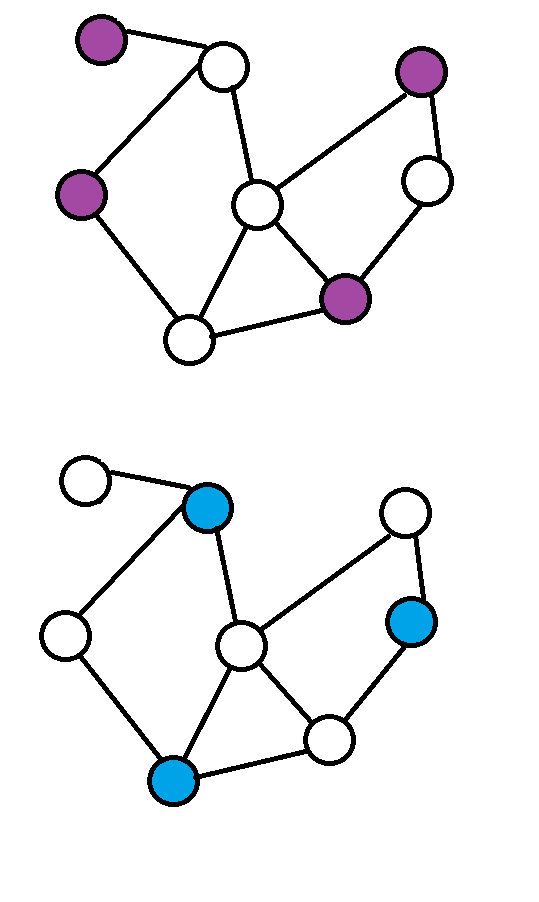
定义:覆盖集中,点数最少的点的点集。
二分图最大匹配
题目让我们将两个点集之间匹配,使得尽量多的点匹配成功。
这里我们讲的是匈牙利算法。
DFS
我们将每个点尽量匹配,只要能配上,就先匹配,被匹配成功的点记录匹配的点。
如果后面的点可以和已经被匹配成功的点匹配,那么尝试被匹配成功的点记录的匹配的点能不能和别的点匹配,如果匹配成功,那么两个点都匹配成功,否则不行。
例子:
假如 $a$ 和 $m,n$ 直接可以匹配(有连边),但是 $b$ 只能和 $m$ 匹配,$c$ 只能和 $n$ 匹配。
$a$ 开始匹配,和 $m$ 尝试,匹配成功,$m$ 记录 $a$,匹配成功点的数量增加。
$b$ 开始匹配,和 $m$ 尝试,$m$ 已经被匹配过了,尝试让记录的匹配点 $a$ 能不能匹配别的,$a$ 可以匹配 $n$,匹配成功。$n$ 记录 $a$,$m$ 记录 $b$,匹配成功点的数量增加。
$c$ 开始匹配,和 $n$ 尝试,$n$ 已经被匹配过了,尝试让记录的匹配点 $a$ 能不能匹配别的,$a$ 可以匹配 $m$,$m$ 被 $b$ 匹配,$b$ 没有点可以匹配了,匹配失败,记录不变,匹配成功点的数量不变。
思路
读入基本信息。
每个节点尝试匹配,统计匹配成功的点。
输出。
代码
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<queue>
#include<vector>
#include<stack>
using namespace std;
int r_r(){//快读
int k=0,f=1;
char c=getchar();
while(!isdigit(c)){
if(c=='-')f=-1;
c=getchar();
}
while(isdigit(c)){
k=(k<<1)+(k<<3)+(c^48);
c=getchar();
}
return k*f;
}
const int o_o=5e4+10;
int n=r_r(),m=r_r(),k=r_r();
int v_v[o_o];//存储节点的已经匹配的点
//链式前向星
struct po{
int n_t;
int v;
}p_p[o_o];
int h_d[o_o],x_p;
int b_b[o_o];//记录是否尝试过当前节点(防止成环)
int a_s;//统计结果
void a_d(int u,int v){//加边
p_p[++x_p].v=v;
p_p[x_p].n_t=h_d[u];
h_d[u]=x_p;
}
bool f_i(int k){
for(int i=h_d[k];i;i=p_p[i].n_t){
int v=p_p[i].v;
if(b_b[v])continue;//已经尝试过了
b_b[v]=1;//标记尝试
if(!v_v[v]||f_i(v_v[v])){//没有匹配或者可以改配
v_v[v]=k;//记录匹配节点
return 1;//匹配成功
}
}
return 0;//匹配失败
}
int main(){
for(int i=1;i<=k;i++){//加边
int u=r_r(),v=r_r();
a_d(u,v);
}
for(int i=1;i<=n;i++){//尝试每个节点
if(f_i(i))a_s++;//尝试成功,累计
memset(b_b,0,sizeof b_b);//清空标记
}
printf("%d",a_s);//输出结果
return 0;
}BFS
网上代码很难找,但是一般情况下,效率比 dfs 高。
和 dfs 的思路一样,也是一个点一个点试。
但是 dfs 是找到一个“可能匹配”的点就尝试,知道搜到“底”,不能搜位置(节点没有其它路或搜到的路都标记过了)。
而 bfs 是采用增广的概念,先将一个节点所有能到达的节点记录(开一个数组),同时这些节点记录是从哪个节点增广的(如果匹配成功,方便回溯更新匹配结果)。
思路
建边(为了方便增广节点区分和表示,将所有的被匹配节点编号续在匹配节点编号之后)。
尝试每个节点(记录基础信息:从哪个点增广的,节点遍历数组……)。
匹配成功后回溯,更新每个节点匹配的点。
统计结果输出。
代码
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<queue>
#include<vector>
#include<stack>
using namespace std;
long long r_r(){//快读
long long k=0,f=1;
char c=getchar();
while(!isdigit(c)){
if(c=='-')f=-1;
c=getchar();
}
while(isdigit(c)){
k=(k<<1)+(k<<3)+(c^48);
c=getchar();
}
return k*f;
}
const int o_o=2e6+10;
int n,m,k;
int p_r[o_o];//从哪个点增广来的
int m_c[o_o];//记录当前节点和哪个节点匹配
int q_e[o_o];//遍历的节点
int t_i,h_i;//下标控制从哪遍历,遍历到哪
int f_i[o_o];//匹配成功的编号
//链式前向星
int v_v[o_o],h_d[o_o],n_t[o_o],x_p;
void a_d(int u,int v){//加边
v_v[++x_p]=v;
n_t[x_p]=h_d[u];
h_d[u]=x_p;
}
int g_a(){
int a_s=0;
for(int i=1;i<=n;i++){
t_i=h_i=0;//初始化
q_e[0]=i;//从 i 节点开始
p_r[i]=0;//初始化来的节点
bool b_p=0;
while(t_i<=h_i){//在增广路内
int u=q_e[t_i++];//读取当前节点
for(int j=h_d[u];j;j=n_t[j]){
int v=v_v[j];
if(f_i[v]==i) continue;
f_i[v]=i;//标记
if(m_c[v]){//已经匹配
p_r[m_c[v]]=u;//记录来的点
q_e[++h_i]=m_c[v];//增广
}else{//没有匹配
int a=u,b=v;//记录来的点和要去的点
int k_k;
while(a){//一直会找,直到找回到 i(初始值为 0)
k_k=m_c[a];//记录匹配的点(要更换匹配)
//互相记录已经匹配
m_c[a]=b;
m_c[b]=a;
a=p_r[a];//返回来的点
b=k_k;//更新为匹配的点(更换匹配)
}
b_p=1;//标记匹配成功返回
break;
}
}
if(b_p)break;//匹配成功返回
}
if(m_c[i]) a_s++;//统计结果
}
return a_s;
}
int main(){
n=r_r(),m=r_r(),k=r_r();
for(int u,v,i=1;i<=k;i++){//加边
u=r_r();
v=r_r()+n;
a_d(u,v);
}
printf("%d",g_a());//输出结果
return 0;
}二分图最大完美匹配
$KM$ 算法。
题目让我们找最大权值的完美匹配,注意是完美匹配的情况下,边权最大。
由于节点的数量非常少,所以可以直接开一个数组维护边权。开一个二维数组将边的初始信息存入。
每个节点进行匹配,将当前点加进来后,遍历整张图边的最大值,记录,接着次大值……直到没有增广路了结束。一路上节点要记录是从哪个节点增广来的,最后要换配(更新匹配的节点),因为最后还要输出匹配的编号。
代码思路
初始化,读入基本信息。
将每个节点进行匹配。
找到图上当前的最大边权。
根据最大边权,处理增广路。
去掉最大权值的边,继续找最大边权,重复上一步。
统计权值,输出。
代码
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<queue>
#include<vector>
#include<stack>
using namespace std;
long long r_r(){//快读
long long k=0,f=1;
char c=getchar();
while(!isdigit(c)){
if(c=='-')f=-1;
c=getchar();
}
while(isdigit(c)){
k=(k<<1)+(k<<3)+(c^48);
c=getchar();
}
return k*f;
}
const long long o_o=1e3+10;
const long long m_a=1e18;
long long n,m;
long long m_p[o_o][o_o];//建立点点之间的边权
long long b_d[o_o];//存储匹配的编号
long long s_s[o_o];//到节点的最小值
long long p_r[o_o];//记录增广的节点(从那个点来的)
long long m_x[o_o];//匹配点集权值
long long m_y[o_o];//被匹配点集权值
bool b_b[o_o];//标记是否遍历过
void f_i(long long u){
//初始化
long long k_k=0;//记录当前处理的节点的编号
long long l_t=0;//记录最优路径的编号
long long x,m_i;//当前处理的节点,最小值
memset(p_r,0,sizeof(p_r));//初始化
for(long long i=1;i<=n;i++)s_s[i]=m_a;//初始化
b_d[0]=u;//从当前节点开始
while(1){
x=b_d[k_k];//找到匹配的节点
m_i=m_a;//初始化最小值
b_b[k_k]=1;//标记
for(long long i=1;i<=n;i++){//枚举所有被匹配的节点
if(b_b[i])continue;//被标记过
if(s_s[i]>m_x[x]+m_y[i]-m_p[x][i]){//更新最小值
//这里边的权值取的是相反数,所以权值越大,值越小
s_s[i]=m_x[x]+m_y[i]-m_p[x][i];//更新最小值
p_r[i]=k_k;//记录来的点
}
if(s_s[i]<m_i){
m_i=s_s[i];//更新最小值
l_t=i;//记录编号
}
}
for(long long i=0;i<=n;i++){//枚举所有节点
if(b_b[i]){//标记过的节点
m_x[b_d[i]]-=m_i;//匹配节点加上最大边权
m_y[i]+=m_i;//被匹配节点减去最大边权
}else s_s[i]-=m_i;//所有节点加上最大边权
//加上最大边权,下次的边权一定小于等于这个边权,可以继续找次大边权
}
k_k=l_t;//处理记录的编号最优边的增广路
if(b_d[k_k]==-1)break;//没有增广路,退出循环
}
while(k_k){//回溯(换配)
b_d[k_k]=b_d[p_r[k_k]];//更新匹配编号
k_k=p_r[k_k];//往回找
}
}
long long k_m(){
//初始化
memset(b_d,-1,sizeof(b_d));//未匹配过的节点的值是 -1
memset(m_x,0,sizeof(m_x));
memset(m_y,0,sizeof(m_y));
for(long long i=1;i<=n;i++){
memset(b_b,0,sizeof(b_b));//清空标记
f_i(i);//匹配 i 节点
}
long long r_s=0;
for(long long i=1;i<=n;i++)
if(b_d[i]!=-1)r_s+=m_p[b_d[i]][i];//统计权值
return r_s;
}
int main(){
n=r_r(),m=r_r();
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)m_p[i][j]=-m_a;//初始化
for(long long i=1;i<=m;i++){
long long u=r_r(),v=r_r(),w=r_r();
m_p[u][v]=w;//边赋权值
}
printf("%lld\n",k_m());//计算最大权值
for(long long i=1;i<=n;i++)//输出匹配结果
printf("%lld ",b_d[i]);
puts("");
return 0;
}
