前置知识:
一般图最大匹配
题目的要求从二分图匹配比那成了一般图匹配,其实和 BFS 版的匈牙利算法想法有些相似:找增广路。但是题目的图变成了一般图,所以就会有环的出现。那么问题的聚焦点就是对环的处理。
环分为奇环和偶环,其中偶环可以“自产自消”但是奇环不行,所以我们重点处理的也是奇环。
偶环:
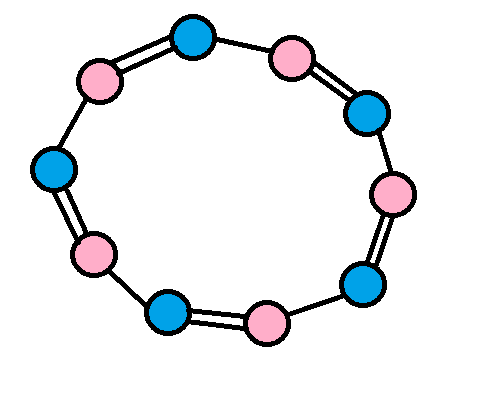
(其中,一条线代表路径,两个点可以互通,两条线代表两个点匹配,一个蓝点匹配一个粉点。)
带花树定义:可以处理图中有奇环的情况,将奇环缩成一个点(算法中叫做一朵花),然后再类似于匈牙利算法通过找增广路来找这个图的最大匹配。
我们不直接讲怎么处理奇环,先讲代码思路,碰见问题再说。
数组初始化,读入基本信息(加边),如果都没有匹配,就先匹配上。
尝试没有匹配的点,能不能让其它点改配,从而让这个点匹配成功。
初始化信息(每个第一次没有匹配的点都会尝试,所以一定要初始化)。
这里我们用的信息有这些:标记该节点是否尝试过匹配,或是否已经加入尝试改配的序列了。
注意:这个数组要记录三中状态:$1$ 尝试换配,$2$ 尝试过的点,$0$ 没有尝试过的点。
想想一下,现在有 $4$ 个点,$a$ 和 $b$ 可以匹配,$b$ 和 $c,d$ 可以匹配,$d$ 和 $c$ 也可以匹配。但是现在,$b$ 和 $c$ 匹配上了(这显然不优)。
我们尝试让 $a$ 匹配,$a$ 可以匹配 $b$ 但是 $b$ 已经匹配了,这是将 $b$ 打上标记 $2$ 代表尝试过的点,而 $c$ 打上标记 $1$ 代表尝试换配的点。因为,如果 $c$ 可以匹配其他的,那么就将 $b$“让”出来了,那么 $a$ 也就匹配成功了,所以 $c$ 入队尝试匹配。
记得开新数组,因为这时的 $b$ 还要存储 $a$,是 $a$ 尝试匹配,这样如果匹配成功了,方便回溯。
发现 $c$ 和 $d$ 还可以匹配,那么就让 $c$ 和 $d$ 匹配,$b$ 被让出来了,利用刚刚开的新数组回溯让 $a$ 和 $b$ 匹配。
- 尝试节点入队,尝试匹配,不断进行标记,如果出现了已经打过标记 $1$ 的节点,那么说明成环了,而且是奇环。
匹配遇见了标记 $1$ 的节点,我们现在遍历的点(尝试换配的点)全是标记为 $1$ 的点,而两个标号为 $1$ 的点相遇了,说明是奇环。如下图所示:
奇环:
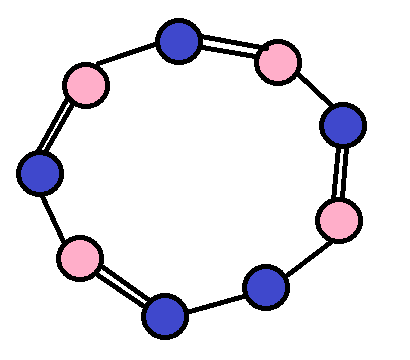
(和上面的偶环的规则一样。这里蓝色节点代表了标记是 $1$。)
上图只是一个奇环,所以可能看不出什么名堂,请看下面这个图:

在第一个小图中可以看到,匹配的并不是最优的,那么我们就要尝试让他更优,我们从红点开始处理,尝试匹配。
(上面的紫虚边代表如果试配成功,那么换配后,紫虚边就换变成黑实边,也就是匹配边,而黑虚边就会消失;而如果匹配失败,黑虚边就会变回黑实边,紫虚边消失。)
最后匹配成功也就让整个环“合理”了(代码中标记的是“逆环”操作(名字乱起的,明白最重要))。
我们上边只是一个奇环,简单的一张图,如果是环套多个环(环中有环),那么怎么处理呢?
首先,要将整个环选出一个祖先(不管大环还是小环,缩完点后,就可以看成点,环套环就可以把里面的环先缩成点,再将外面的环缩成点。),大体流程如下(为了减少篇幅画一块了,先看左边的一列):
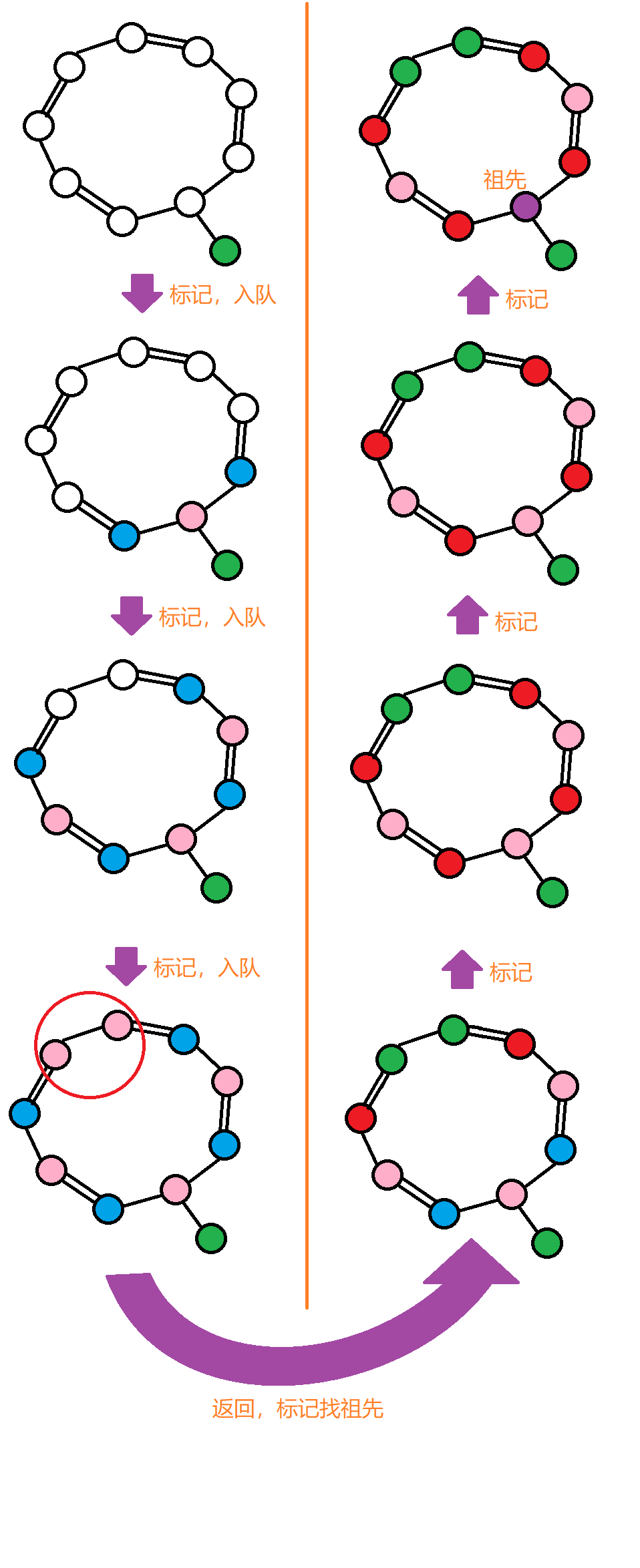
注意:找祖先的时候,要将两个“碰头”的点同时往回找。如果只让一个点往回找的话,就直接回到绿点(开始的地方)了。
如果匹配成功要记得换配(更新匹配关系)。
统计结果,输出即可。
细节详见代码。
代码思路整理
数组初始化,读入基本信息。
尝试没有匹配的点。
每个点匹配都要初始化信息。
尝试更多匹配,匹配成功换配。
统计结果,输出。
代码
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<queue>
#include<vector>
#include<stack>
using namespace std;
long long r_r(){//快读
long long k=0,f=1;
char c=getchar();
while(!isdigit(c)){
if(c=='-')f=-1;
c=getchar();
}
while(isdigit(c)){
k=(k<<1)+(k<<3)+(c^48);
c=getchar();
}
return k*f;
}
const int o_o=2e5+10;
queue<int>q_q;
int n,m;
int a_s;//统计结果
int l_k[o_o];//记录和哪个点匹配
int b_b[o_o];//标记 1 尝试换配,2 尝试过的点,0 没有尝试过的点
int f_a[o_o];//记录父节点
int p_r[o_o];//记录从那个点来的
int x_x;//环缩点后的标号
int g_h[o_o];//共环的编号
//链式前向星
struct po{
int v;
int n_t;
}p_p[o_o];
int h_d[o_o],x_p;
void a_d(int u,int v){//加边
p_p[++x_p].v=v;
p_p[x_p].n_t=h_d[u];
h_d[u]=x_p;
}
void n_w(int x){//换配
if(!x)return ;
n_w(l_k[p_r[x]]);//一直走到头
//换配
l_k[x]=p_r[x];
l_k[p_r[x]]=x;
}
int f(int k){//找父节点
if(k==f_a[k])return k;
return f_a[k]=f(f_a[k]);//路径压缩
}
int l_c(int x,int y){
x_x++;//开新点(环缩点)
while(1){
x=f(x);//上爬,爬到父节点(如果不是自己的话,相当于直接出环)
if(g_h[x]==x_x)return x;
//跑到已经标记过的点了,定义当前点为这个环的祖先
else if(x)g_h[x]=x_x;//更新节点标记
x=p_r[l_k[x]];//更新为当前节点匹配的节点的来的点
//下一个可能换配的点,即标记 b_b 为 1 的点
swap(x,y);//交换标号,两头一起跑,可以成环相遇
//如果只有一个点跑就跑回起点了
}
}
void s_k(int x,int y,int f_f){
while(f(x)!=f_f){//不是子节点
p_r[x]=y;//更新记录来的点
y=l_k[x];//记录匹配的点
f_a[x]=f_a[y]=f_f;//匹配的一对点更新父节点
if(b_b[y]==2){//遍历过
b_b[y]=1;//标记
q_q.push(y);//入队尝试
}
x=p_r[y];//更新到 y 的点
}
}
int b_s(int x){
for(int i=1;i<=n;i++){//初始化信息
b_b[i]=0;
p_r[i]=0;
f_a[i]=i;//初始化父节点
}
b_b[x]=1;//标记
q_q=queue<int>();//清空队列
q_q.push(x);//将当前节点入队
int f_f;
while(!q_q.empty()){
int k=q_q.front();//提取队头
q_q.pop();
for(int i=h_d[k];i;i=p_p[i].n_t){
int v=p_p[i].v;
if(b_b[v]==1){//标记过,尝试匹配路径成环了
f_f=l_c(k,v);//记录环的公共祖先
//逆环尝试
s_k(k,v,f_f);
s_k(v,k,f_f);
}else if(!b_b[v]){//没有标记过
p_r[v]=k;//记录来的点
b_b[v]=2;//标记到过节点,但是不是尝试换配的节点
if(!l_k[v]){//当前节点没有匹配过
n_w(v);//换配
return 1;//匹配成功
}else {//当前节点已经匹配
b_b[l_k[v]]=1;//和目标匹配的节点标记,尝试换配
q_q.push(l_k[v]);//入队,尝试匹配其他节点
//如果它能匹配成功别的点,就能把这个点“让”出来
}
}
}
}
return 0;
}
int main(){
n=r_r(),m=r_r();
for(int i=1;i<=m;i++){
int a=r_r(),b=r_r();
//加边
a_d(a,b);
a_d(b,a);
if(!l_k[a]&&!l_k[b]){//两个点都没有匹配,先匹配上
l_k[a]=b;//记录匹配的点
l_k[b]=a;
a_s++;//统计匹配对数
}
}
for(int i=1;i<=n;i++)
if(!l_k[i]&&b_s(i))a_s++;
//节点未匹配,尝试匹配,如果匹配成功,统计结果
printf("%d\n",a_s);//输出匹配成功的对数
for(int i=1;i<=n;i++)printf("%d ",l_k[i]);//输出匹配编号
return 0;
}
