导数
连续 $\Delta x\to 0,\Delta y\to 0$。
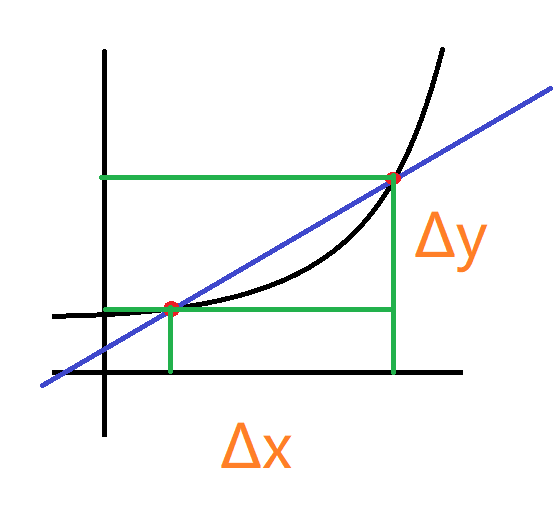
变化率:$x_0\to x_0+\Delta x,f(x_0)\to f(x_o+\Delta x)$
$y=f(x)$,在 $x_0$ 邻域 $U(x_0)$ 有定义 $\Delta x\not= 0,x_0+\Delta x\in U(x_0)$
导数四种符号:
平常有时候也写成:
表示对 $x_0$ 求导。
切线斜率:
常用导数公式
$n$ 为实数。
$c$ 为常数。
可导
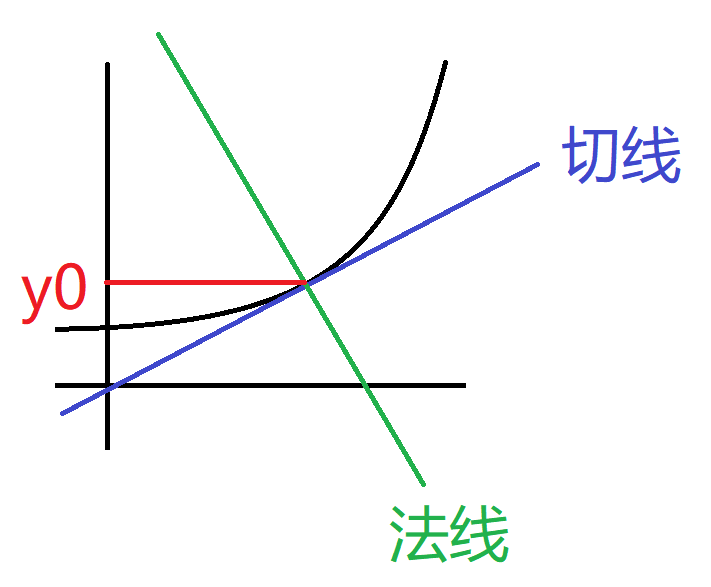
切线:
法线:
左可导,$f^{‘}_{-}{(x_0)}$
右可导,$f^{‘}_{+}{(x_0)}$
$[a,b]$
可导。
可导 $\Leftrightarrow$
可导必连续
练习:
$y=\sqrt[3]{x}$ 在 $x=0$ 处。
求导法则
- 加法:
$u(x),v(x)$ 可导。
左边是有限个函数。
- 练习:
- 乘法:
设 $c$ 是常数:$(cu)^{‘}=c^{‘}u+cu^{‘}=cu^{‘}$
- 除法:
- 练习:
- 反函数:
$y=f(x),x=g(y)$(互为反函数)
$g^{‘}(y)=\frac{1}{f^{‘}(x)}$(互为倒数)
$y=a^x$ 反函数: $x=\log_a{y}(y>0)$
- 复合函数:
这就是“链式法则”。
- 练习:
高阶导数
这是二阶导数。
三阶导数:
四阶导数:
$4$ 阶及以上的导数直接写数字即可,注意加括号,和幂区分。
$n$ 阶导数:
- 练习:
- 对于某个未知数求导要表明!
求 $\dfrac{d^2y}{dx^2}$ 即 $f^{‘’}{(x)}$($r$ 是常数)。
如果用一般的思路用 $y$ 去表达 $x$ 会发现要对式做很复杂的调整,所以我们直接整体求导:
两边同时对 $x$ 求导:
- 第四种求导表示法(上面介绍的四种书写方法的最后一种):
这里我们一般采用第一种写法,但是要知道上面的等式成立。
这里的时候 $\frac{dx}{dt}$ 我们用的是整体思想,但是其实 $dx$ 和 $dt$ 是个体,在后面的微分中介绍。意义是 $dx$ 对于 $dt$ 求导。
导数规律小结
- 降幂:
- 自然对数:
- 分式:
- 三角函数:
- 分配律:

