微分基础

导数

微分

$$\Delta x,\Delta y=y(x_0+\Delta x)-y(x_0)$$ $$y=e^x,x:1\to 1.01,\Delta y=e^{1.01}-e^1$$

人工不好计算出 $\Delta y$ 的值，并且，在现实生活中不需要那么高的精度。所以我们可以去近似值。

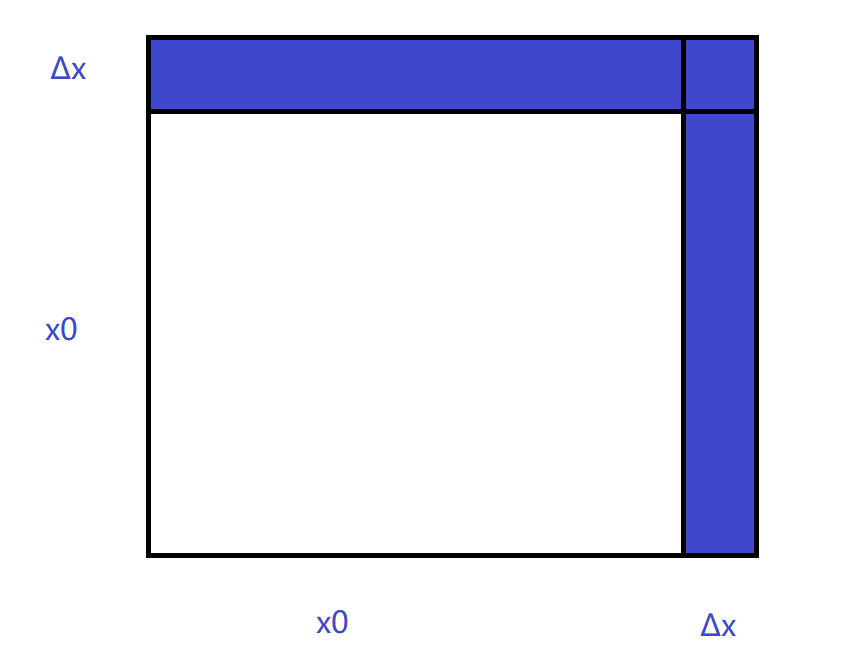
原来，我们有边长为 $x_0$ 的正方形，现在我们将它扩建，边长增加 $\Delta x$，那么

$$\Delta S=(x_0+\Delta x)^2-x_0^2=2(x_0+\Delta x)\Delta x$$ $$=2x_0\Delta x+(\Delta x^2)$$ $$\because \Delta x\to 0$$ $$\therefore \approx 2x_0\Delta x$$

我们舍去了 $(\Delta x)^2$，不难发现 $\Delta x$ 越大，结果就越不精准，所以一般 $\Delta x$ 会去很小，保证结果在精度范围内。（$x_0$ 是常量，$\Delta x$ 是变量）。

$f(x)$ 在邻域范围内有定义，$(x+\Delta x)$ 在邻域内。

$$\Delta y=f(x_0+\Delta x)-f(x_0)$$

可以表示为：

$$\Delta y=A\Delta x+o(\Delta x)$$

$\Delta y$：精确值，$dy$：近似值（$o(\Delta x)$ 舍去）。

$f(x)$ 在 $x_0$ 可微 $\Leftrightarrow$ $dy=f^{‘}{(x_0)}\Delta x$

其中，上文中的 $A=f^{‘}{(x_0)}$

$\Delta x=dx,\Delta y\approx dy$

$\frac{dy}{dx}=f^{‘}{(x)}$ 导数也叫“微商”。

• 练习：

$f(x)=x^2$ 在 $x=2$ 处的微分，$\Delta x=0.01$，该变量和微分值。

$$dy=2x\Delta x,\left.dy\right|_{x=2}=2\Delta x,\Delta x=0.01,dy=0.04$$

微分值。

$$\Delta y=(2.01)^2-2^2=0.0401$$

精确值。

为什么会出现细微的差距呢？因为我们舍了 $(\Delta x)^2$。

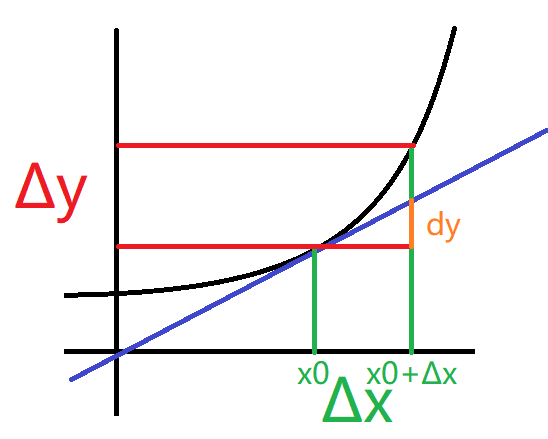
图中形象的区别了 $\Delta y$ 和 $dy$ 的差距是如何出现的，我们在 $x_0$ 处求了导数，利用导数找到在 $x_0+\Delta x$ 处的 $y$ 值。所以和真实出现了偏差。

$$\Delta y=A\Delta x+o(\Delta x)$$ $$\Delta y\approx dy$$ $$dy=A\Delta x=f^{'}{(x)}dx$$

• 基本公式：$dc=c^{‘}dx$

四则运算

$$d(u\pm v)=du\pm dv$$ $$d(u+v)=(u+v)^{'}dx=u^{'}dx+v^{'}dx=du+dv$$ $$d(uv)=udv+vdu$$ $$d(cu)=cdu$$

（$c$ 是常数）。

$$d(\frac{u}{v})=\frac{vdu-udv}{v^2}$$ $$(\frac{u}{v})^{'}=\frac{u^{'}v-v^{'}u}{v^2}$$

• 练习：

• $1$：

$$y=x^2+\ln x-3^x$$ $$dy=dx^2+d\ln x-d3^x$$ $$=2xdx+\frac{1}{x}dx-3^x(\ln 3)dx$$ $$=(2x+\frac{1}{x}-3^x\ln 3)dx$$ $$dy=y^{'}dx=(2x+\frac{1}{x}-3^x\ln 3)dx$$

• $2$：

$$y=x^3e^x\sin x$$ $$d(uvw)=vwdu+uwdv+uvdw$$ $$dy=e^x\sin x d x^3+x^3\sin d e^x+x^3 e^x d\sin x$$ $$=(3e^x\sin x x^2+x^3\sin x e^x+x^3e^x\cos x)dx$$

• $3$：

$$y=\frac{x^2+1}{x+1},dy=d(\frac{x^2-1+2}{x+1})=d(x-1+\frac{2}{x+1})$$ $$=dx+d(\frac{2}{x+2})=dx-\frac{2}{(x+1)^2}dx$$

一阶微分形式不变性

$$y=f(x)$$

$x$ 是自变量 $dy=f^{‘}{(x)}dx$

$x$ 是函数 $x=g(k),y=f(g(k))$

$$dy=f^{'}{(x)}g^{'}{(k)}dk=f^{'}{(x)}dx$$ $$dx=g^{'}{(x)}dk$$

• 练习：

• $1$：

$$y=e^{\sin^2 x}$$ $$dy=de^{\sin^2 x}=e^{\sin^2 x}d\sin^2 x$$ $$=e^{\sin^2 x}2\sin(x) d\sin (x)$$ $$=e^{\sin^2 x}2\sin(x) \cos (x)dx$$

• $2$：

$$y=\ln(x+\sqrt{1+x^2})$$ $$dy=\frac{1}{x+\sqrt{1+x^2}}d(x+\sqrt{1+x^2})$$ $$=\frac{1}{x+\sqrt{1+x^2}}(dx+\frac{d(1+x^2)}{2\sqrt{1+x^2}})$$ $$=\frac{1}{x+\sqrt{1+x^2}}(dx+\frac{2xdx}{2\sqrt{1+x^2}})$$ $$=\frac{1}{x+\sqrt{1+x^2}}(1+\frac{2x}{2\sqrt{1+x^2}})dx$$ $$=\frac{1}{\sqrt{1+x^2}}dx$$

• $3$ 复杂：

$$x^2+2xy-y^2=2x$$

两边同时对 $x$ 求导：

$$2x+2y+2xy^{'}-2yy^{'}=2$$ $$y^{'}=\frac{1-x-y}{x-y}$$ $$dy=\frac{1-x-y}{x-y}dx$$

也可以用今天刚学的微分方法：

$$2xdx+2ydx+2xdy-2ydy=2dx$$ $$(2x-2y)dy=(2-2x-2y)dx$$ $$dy=\frac{2-2x-2y}{2x-2y}dx$$ $$dy=\frac{1-x-y}{x-y}dx$$

• 总结：

$$\Delta y\approx dy=f^{'}{(x_0)}\Delta x$$ $$f(x_0+\Delta x)-f(x_0)\approx f^{'}{(x_0)}\Delta x$$ $$f(x_0+\Delta x)\approx f(x_0)+f^{'}{(x_0)}\Delta x$$

$|\Delta x|$ 取得很小。

• 练习：

$f(x)=2x^2-3x,x_0=5,\Delta x=0.2,\Delta x=1$ 分别求 $\Delta y,dy$。

$$\Delta y=f(5+\Delta x)-f(5)=17\Delta x+2(\Delta x)^2$$ $$dy=17\Delta x$$ $$\Delta x=0.2,\Delta y=3.48,dy=3.4$$ $$\Delta x=1,\Delta y=19,dy=17$$

可以直观的看出 $\Delta x$ 对于精度的影响。

常见微分

取 $x_0=0,\Delta x=x$

$$f(x)\approx f(0)+f^{'}{(0)}x$$

• $1$：

$$\sqrt[n]{1\pm x}\approx 1\pm \frac{x}{n}$$ $$\sqrt[n]{1+x} \approx f(0)+f^{'}{(0)}x=1+\frac{x}{n}$$

• $2$：

$$\sin x\approx x$$ $$\lim_{x\to 0}{\frac{\sin x}{x}}=1$$

• $3$：

$$\tan x=x$$

• $4$：

$$e^x\approx 1+x$$

• $5$：

$$\ln{(1+x)}\approx x$$

• $6$：

$$\frac{1}{1+x}\approx 1-x$$ $$1\approx 1-x^2$$

• $7$：

$$\arcsin x\approx x$$

• $8$：

$$\arctan x\approx x$$

利用微思想求值

$$\sqrt[3]{997}=\sqrt[3]{1000-3}=10\sqrt[3]{1-0.003}\approx 10\times (1-\frac{0.003}{3})=9.99$$ $$\ln{1.03}=\ln{(1+0.03)}\approx 0.03$$

现在我们可以通过学习的知识对一些无理数求大概的值了。