并查集
主要是用来,快速查询两个节点是否是同族的(或者说,在同一个集合里)。
集合合并
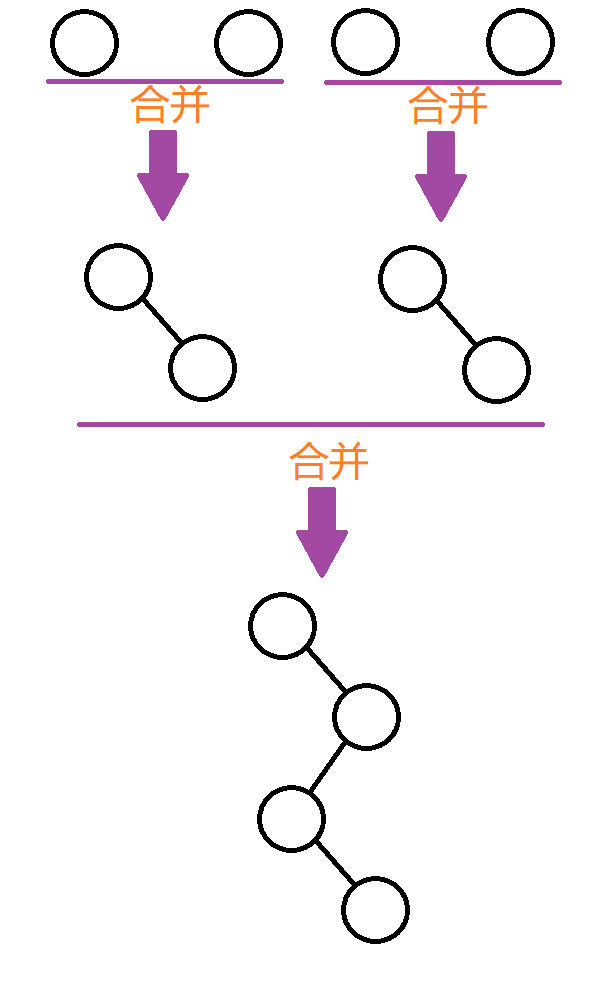
简单来讲,就是将几个节点“联系”在一起,而为了方便确认它们确实“联系”在一起,要推选出一个代表(祖先),这样只要确定代表是否相同,那么就能确定是否“联系”在了一起。
代码
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<string>
#include<cstring>
#include<cctype>
using namespace std;
int r_r(){
int x=0,f=1;
char c=getchar();
while(!isdigit(c)){
if(c=='-')f=-1;
c=getchar();
}
while(isdigit(c)){
x=(x<<1)+(x<<3)+(c^48);
c=getchar();
}
return x*f;
}
const int o_o=1e6+10;
int f_a[o_o];
int f(int k){//找祖先
if(k==f_a[k])return k;
return f_a[k]=f(f_a[k]);//一边找,一边存(路径压缩)
}
void b_g(int x,int y){//合并
int f_x=f(x),f_y=f(y);//找父节点
if(f_x!=f_y)f_a[f_x]=f_y;//不在一个集合中,并入同一个集合
}
void f_i(int x,int y){
int f_x=f(x),f_y=f(y);//找父节点
if(f_x!=f_y)puts("N");//不在一个集合
else puts("Y");//在一个集合
}
int main(){
int n=r_r(),m=r_r();
for(int i=1;i<=n;i++)f_a[i]=i;//初始化父节点
for(int i=1;i<=m;i++){//处理所有询问
int op=r_r();//读入询问类型
int x=r_r(),y=r_r();//读入要处理的两个元素
if(op==1)b_g(x,y);//合并
else f_i(x,y);//查找是否在一个集合中
}
return 0;
}按秩合并
不难发现,其实在合并的时候有很多种方式,取决于合并的先后顺序,但是可能会被数据卡成一条链,此时的复杂度和暴力基本没区别。
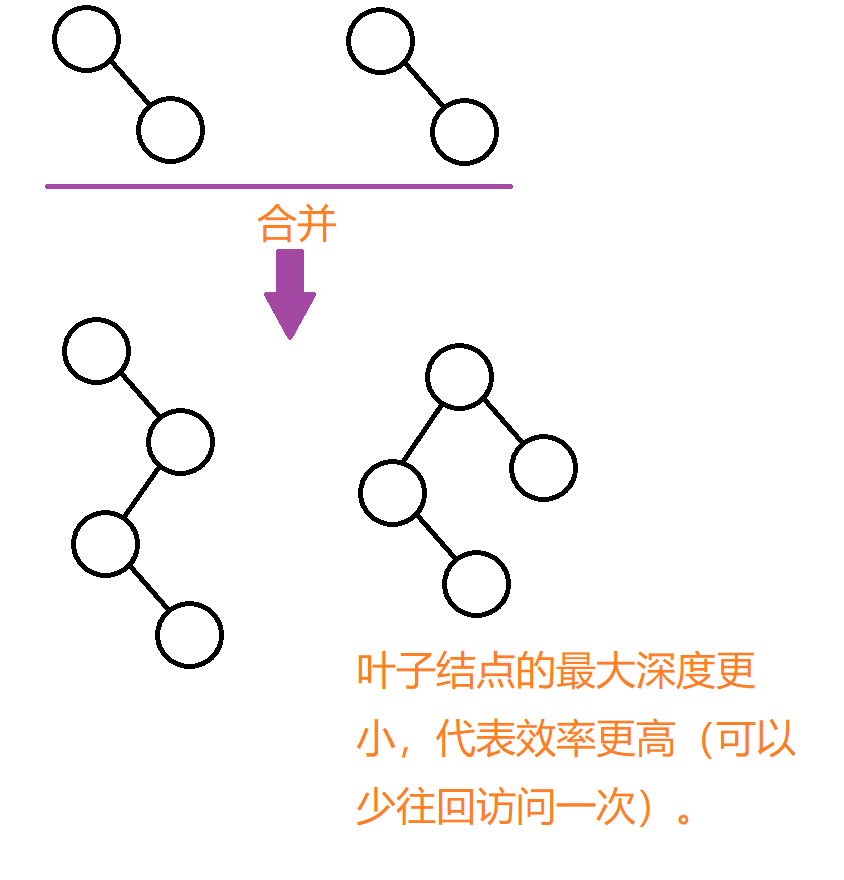
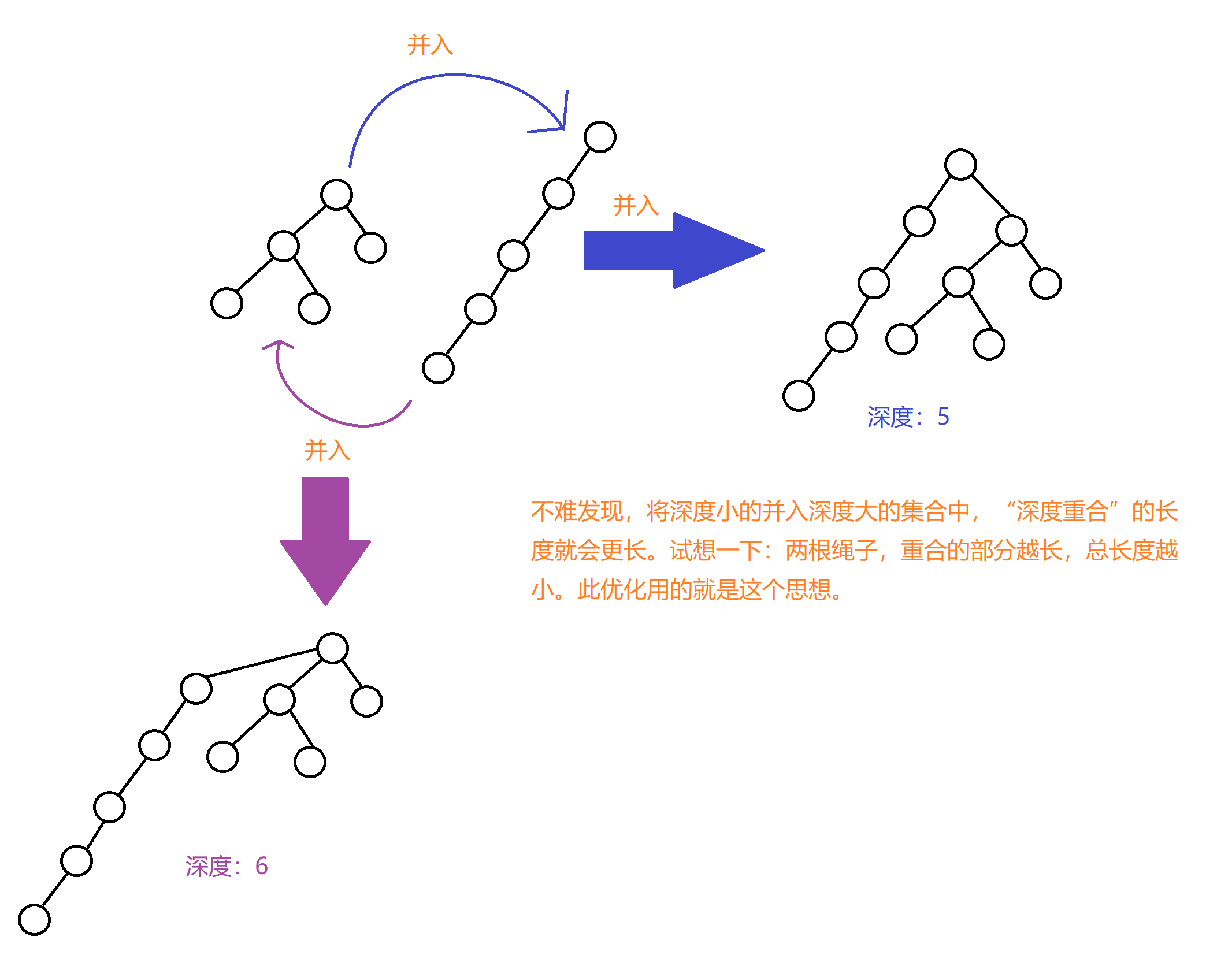
我们就可以给每个集合多一个信息:大小。根据两个要合并的集合,判断谁的深度更大就并到谁那里。
因为并到更深的集合中,最低深度会更优(最低深度会更浅)。
代码
#include<iostream>
#include<cmath>
#include<cstring>
#include<string>
#include<algorithm>
#include<cstdio>
#include<queue>
using namespace std;
int r_r(){//快读
int x=0,f=1;
char c_c=getchar();
while(!isdigit(c_c)){
if(c_c=='-')f=-1;
c_c=getchar();
}
while(isdigit(c_c)){
x=(x<<1)+(x<<3)+(c_c^48);
c_c=getchar();
}
return x*f;
}
const int o_o=1e6+10;
int f_a[o_o];//父节点
int s_z[o_o];//集合大小
int f(int k){//查找父节点
if(k==f_a[k])return k;
else return f_a[k]=f(f_a[k]);//路径压缩
}
int main(){
int n=r_r(),m=r_r();
for(int i=1;i<=n;i++){
f_a[i]=i;//初始化父节点
s_z[i]=1;//初始化集合大小
}
while(m--){
int op=r_r(),x=r_r(),y=r_r();
x=f(x),y=f(y);//找祖先(集合)
if(op==1){
if(x==y)continue;//在一个集合中
//将集合小的集合并入子树大的集合(缩短路径)
if(s_z[x]>=s_z[y]){
s_z[x]+=s_z[y];
f_a[y]=x;
}else {
s_z[y]+=s_z[x];
f_a[x]=y;
}
}else {//判断是否同集合
if(x!=y)puts("N");
else puts("Y");
}
}
return 0;
}关押罪犯
我们知道的是罪犯之间的冲突关系,每个冲突关系会有怨恨值,我们要是最大怨恨值最小。
我们不知道罪犯最优(怨恨值最小)的情况下在哪个监狱,但是我们有他们的关系,就可以先“确定”一些出冲突保证不会发生(将会产生冲突的两个人分别“并入”会和他们分别产生冲突的集合中)。假如有 $1,2,3$ 号,$1$ 和 $2$ 冲突,$2$ 和 $3$ 冲突,那么就将 $1,3$ 并入到一个集合(监狱)中。
因为我们要使最后的怨气值最小,所以可以将所有关系根据怨气的大小,从大到小排序,尽量确保不会发生冲突,当最后必须并成一个集合时,就是冲突必然发生时,这是就可以直接输出怨气值了(我们已经尽力了,将怨气值从大到小排序,所以这是最优解)。
代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
#include<cmath>
#include<queue>
#include<map>
#include<set>
#include<stack>
using namespace std;
long long r_r(){
long long x=0,f=1;
char c=getchar();
while(!isdigit(c)){
if(c=='-')f=-1;
c=getchar();
}
while(isdigit(c)){
x=(x<<1)+(x<<3)+(c^48);
c=getchar();
}
return x*f;
}
const int o_o=1e5+10;
struct po{
int x;
int y;
int z;
}p_p[o_o];//每个罪犯基本信息
int n,m;
int f_a[o_o];//父节点
int c_t[o_o];//记录会冲突的人
bool cmp(po f_a,po c_t){
return f_a.z>c_t.z;//按怨气值从大到小排序
}
int f(int x){//找父节点
if(f_a[x]==x) return x;
return f_a[x]=f(f_a[x]);//路径压缩
}
void b_g(int x,int y){//合并集合
x=f(f_a[x]);
y=f(f_a[y]);
f_a[x]=y;//更新父节点
}
bool f_i(int x,int y){//查找是否自同一集合中
x=f(x);
y=f(y);
if(x==y) return 1;
return 0;
}
int main(){
n=r_r(),m=r_r();
for(int i=1;i<=n;i++)f_a[i]=i;//初始化父节点
for(int i=1;i<=m;i++)//读取基本信息
p_p[i].x=r_r(),p_p[i].y=r_r(),p_p[i].z=r_r();
sort(p_p+1,p_p+m+1,cmp);//按怨气值排序
for(int i=1;i<=m+1;i++){
if(f_i(p_p[i].x,p_p[i].y)){//出现冲突,尽力了,输出结果
printf("%d",p_p[i].z);
break;
}else{//未出现冲突
if(!c_t[p_p[i].x])c_t[p_p[i].x]=p_p[i].y;//记录可以起冲突的人
else b_g(c_t[p_p[i].x],p_p[i].y);//将可以起冲突的人合并(贪心)
if(!c_t[p_p[i].y])c_t[p_p[i].y]=p_p[i].x;//互相记录
else b_g(c_t[p_p[i].y],p_p[i].x);//同样合并(贪心)
}
}
return 0;
}断罪者
前置知识:
题目要我们实现并查集的三个操作:删点,单点修改,合并集合(注意:题目中的四种操作只会有后三种操作)。
而对于死亡方式,我们只需要存储最大的罪恶值,单独讨论即可。
思路
清空,初始化数据(注意是多测)。
读入基本信息。
在处理单点修改时,题目要我们找到最大的罪恶值进行修改,那么我们就要维护最大值,这里用的方法是左偏树。
我们用左偏树来维护罪恶值的大根堆。
- 删点:
将节点的基础信息清空(罪恶值,左右子树节点记号,还有左右子树的父节点变成其本身),并更新左偏树,这时我们需要有基础操作:合并左右子树。就是左偏树的基本操作。
- 合并左偏树:
按照罪恶值建成一个大根堆的左偏树,我们只要快速求最大值。其他的和左偏树没变化。
- 单点修改:
找到目标集合的祖先节点,也就是我们维护的左偏树的根节点(最大罪恶值节点)根据要求更新。更新完后,将节点删除。
- 集合合并:
将目标编号的祖先找到左偏树子树合并即可。
- 去世方式:
将所有罪恶值统计一遍,注意设一个数组判重,并记录最大的罪恶值。这样操作 $2,3$ 就变成了,减去最大值和加上最大值。
最后根据题目要求输出即可。
代码
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<string>
#include<cstring>
#include<cctype>
using namespace std;
long long r_r(){//快读
long long x=0,f=1;
char c=getchar();
while(!isdigit(c)){
if(c=='-')f=-1;
c=getchar();
}
while(isdigit(c)){
x=(x<<1)+(x<<3)+(c^48);
c=getchar();
}
return x*f;
}
const int o_o=1e7+10;
long long t=r_r(),w=r_r(),k=r_r();
long long v_v[o_o];//每件事的罪恶值
long long d_p[o_o];//左偏树叶子结点深度
bool b_b[o_o];//标记,去重
long long f_a[o_o];//存父节点
long long l_i[o_o];//存结点左子树编号
long long r_i[o_o];//存结点右子树编号
long long f(long long x){//查找祖先节点
if(f_a[x]==x)return x;
return f_a[x]=f(f_a[x]);
}
long long b_g(long long x,long long y){//合并子树
if(!x||!y)return x+y;//存在空叶子,直接合并
if(v_v[x]<v_v[y]||(v_v[x]==v_v[y]&&x>y))swap(x,y);
//保证左子树罪恶值小于右子树罪恶值
r_i[x]=b_g(r_i[x],y);//右节点和右子节点继续比较,并更新根节点
if(d_p[l_i[x]]<d_p[r_i[x]])swap(l_i[x],r_i[x]);
//保证左子树的深度不小于右子树深度
f_a[l_i[x]]=f_a[r_i[x]]=f_a[x]=x;//更新父节点
d_p[x]=d_p[r_i[x]]+1;//更新深度
return x;//返回根节点编号
}
void d_l(long long x){
long long l=l_i[x],r=r_i[x];//记录左右子树
//更新父节点
f_a[l]=l;
f_a[r]=r;
l_i[x]=r_i[x]=d_p[x]=0;//清空记录
b_g(b_g(l,r),f(x));//合并左右子树
}
int main(){
for(int i=1;i<=t;i++){
//初始化基础信息
d_p[0]=0;
f_a[0]=0;
l_i[0]=r_i[0]=0;
memset(b_b,0,sizeof(b_b));
long long n=r_r(),m=r_r();
for(int i=1;i<=n;i++){
v_v[i]=r_r();//读入罪恶值
f_a[i]=i;//初始化父节点
r_i[i]=l_i[i]=d_p[i]=0;//初始化信息
}
for(int i=1;i<=m;i++){
long long t_p=r_r(),x=r_r();
if(t_p==4){
long long y=r_r();
x=f(x);//祖先节点
y=f(y);//祖先节点
if(x==y)continue;//已经在一个集合了,不用合并了
b_g(x,y);//合并子树
}else if(t_p==2){
v_v[x]=0;//清零
d_l(x);//删点
}else {
long long y=r_r();
x=f(x);//祖先节点(罪恶值最大节点)
v_v[x]=max(v_v[x]-y,0ll);//如果够减直接减,否则清零
d_l(x);//删点
}
}
long long s_m=0,m_a=0;
for(int i=1;i<=n;i++){
long long g_g=f(i);//祖先节点
if(b_b[g_g])continue;//已经标记过
b_b[g_g]=1;//标记
m_a=max(m_a,v_v[g_g]);//记录最大值
s_m+=v_v[g_g];//记录罪恶值的和
}
if(w==2)s_m-=m_a;//免除最大罪恶值
else if(w==3)s_m+=m_a;//最大罪恶值翻倍
//根据规定输出
if(!s_m)printf("Gensokyo 0\n");
else if(s_m>k)printf("Hell %lld\n",s_m);
else printf("Heaven %lld\n",s_m);
}
return 0;
}可持久化并查集
复习一下:主席树
因为有历史信息的调取,所以我们将每个操作最为一个时间点来存储,每回“撤销”时,就直接调用历史的节点信息即可,注意:我们不会改节点,只是一直在开新节点存储信息。
代码
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<string>
#include<cstring>
#include<cctype>
using namespace std;
int r_r(){//快读
int x=0,f=1;
char c=getchar();
while(!isdigit(c)){
if(c=='-')f=-1;
c=getchar();
}
while(isdigit(c)){
x=(x<<1)+(x<<3)+(c^48);
c=getchar();
}
return x*f;
}
const int o_o=1e7+10;
int n,m;
int f_a[o_o];//父节点
int d_p[o_o];//集合最深节点深度
struct po{
int l,r;//记录左右子树根节点编号
}t_r[o_o];
int g_g[o_o];//每个时间点为根节点的标号
int x_p;//赋予新节点编号
void b_t(int &k,int l,int r){
k=++x_p;//开新节点
if(l==r){
f_a[k]=l;//初始化父节点
return;
}
int m_i=l+r>>1;
b_t(t_r[k].l,l,m_i);//左子树
b_t(t_r[k].r,m_i+1,r);//右子树
}
void u_p(int &k,int l_t,int l,int r,int x,int f){
k=++x_p;//开新节点
if(l==r){//叶子结点(父节点)
f_a[k]=f;//更新父节点
d_p[k]=d_p[l_t];//更新深度
return;
}
//继承左右子树信息
t_r[k].l=t_r[l_t].l;
t_r[k].r=t_r[l_t].r;
int m_i=l+r>>1;
if(x<=m_i) u_p(t_r[k].l,t_r[l_t].l,l,m_i,x,f);//在左子树
else u_p(t_r[k].r,t_r[l_t].r,m_i+1,r,x,f);//在右子树
}
int f_i(int k,int l,int r,int x){
if(l==r) return k;//找到叶子结点(父节点)
int m_i=l+r>>1;
if(x<=m_i) return f_i(t_r[k].l,l,m_i,x);//在左子树
else return f_i(t_r[k].r,m_i+1,r,x);//在右子树
}
void a_d(int k,int l,int r,int x){
if(l==r){//找到子叶(父节点)
++d_p[k];//更新深度
return;
}
int m_i=l+r>>1;
if(x<=m_i) a_d(t_r[k].l,l,m_i,x);//在左子树
else a_d(t_r[k].r,m_i+1,r,x);//在右子树
}
int f(int k,int x){
int f_x=f_i(k,1,n,x);//找父节点
if(x==f_a[f_x]) return f_x;//父节点是本身返回父节点
return f(k,f_a[f_x]);//继续找
}
int main() {
n=r_r(),m=r_r();
b_t(g_g[0],1,n);//初始化建树(确定区间左右范围)
for(int i=1;i<=m;++i){
int op=r_r();
if(op==1){
g_g[i]=g_g[i-1];//记录历史情况(在此基础上处理)
int a=r_r(),b=r_r();
int f_1=f(g_g[i],a);//更新为祖先
int f_2=f(g_g[i],b);
if(f_a[f_1]==f_a[f_2]) continue;//已经在一个集合中,不用再合并
if(d_p[f_1]>d_p[f_2]) swap(f_1,f_2);
//最大深度小的并入最大深度大的(和并查集优化一个道理)
u_p(g_g[i],g_g[i-1],1,n,f_a[f_1],f_a[f_2]);
//更新合并结束后的结果
if(d_p[f_1]==d_p[f_2]) a_d(g_g[i],1,n,f_a[f_2]);
//如果深度相同,那么深度要注意 +1(一棵树只能并在另一棵树下面)
}else if(op==2){
int k=r_r();
g_g[i]=g_g[k];//回到之前的状态(直接记录根节点即可)
}else {
g_g[i]=g_g[i-1];//记录历史情况(在此基础上处理)
int a=r_r(),b=r_r();
int f_1=f(g_g[i],a);//更新为祖先
int f_2=f(g_g[i],b);
if(f_a[f_1]==f_a[f_2]) puts("1");//祖先相同,在同一集合
else puts("0");//祖先不同,不在同一集合
}
}
return 0;
}
