基础几何

凸包

• 叉积

在平面中我们为了度量一条直线的倾斜状态，为引入倾斜角这个概念。

而通过在直角坐标系中建立 $\tan a=k$，我们实现了将几何关系和代数关系的衔接，这其实也是用计算机解决几何问题的一个核心。

计算机做的是数值运算，因此你需要做的就是把几何关系用代数关系表达出来。

而在空间中，为了表示一个平面相对空间直角坐标系的倾斜程度，我们利用一个垂直该平面的法向量来度量(因为这转化成了描述直线倾斜程度的问题)。

• 求解三角形（平行四边形）面积

$$\lvert \vec{a}\times \vec{b}\rvert =\lvert \vec{a}\rvert\times \lvert\vec{b}\rvert\times\sin \theta$$ $$S_{\Delta ABC}=\frac{1}{2}\vec{\lvert AB\rvert }\vec{\lvert AC\rvert }\sin A = \frac{1}{2}\lvert \vec{AB}\times \vec{AC}\rvert$$

• 判断 某一点在直线左右侧：

• 若$a\times b>0$ , 则 $a$ 在 $b$ 的顺时针方向。

• 若$a\times b<0$ , 则 $a$ 在 $b$ 的逆时针方向。

• 若$a\times b=0$ , 则 $a$ 与 $b$ 共线，但可能同向也可能反向。

• 凸包定义为：

平面的一个子集 $S$ 被称为是“凸”的，当且仅当对于任意两点 $p$，$s ∈S$，线段 $ps$ 都完全属于 $S$。（平面凸包定义）

P2742【模板】二维凸包

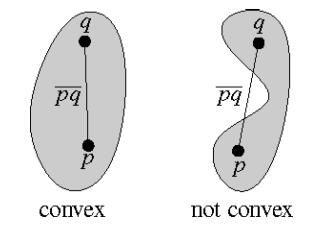
注意判重！

代码

#include<iostream>
#include<cstdlib>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<queue>
#include<vector>
#include<bitset>
#include<stack>
#include<map>
using namespace std;
long long r_r(){//快读 
  long long k=0,f=1;
  char c=getchar();
  while(!isdigit(c)){
    if(c=='-')f=-1;
    c=getchar();
  }
  while(isdigit(c)){
    k=(k<<1)+(k<<3)+(c^48);
    c=getchar(); 
  }
  return k*f;
}
const int o_o=1e6+10;
long long n;
struct po{//记录节点信息 
  double x;
  double y;
}p_p[o_o];
long long s_s[o_o],x_s;
bool cmp(po a,po b){//先按 x 从小到大排序，如果 x 相同，按 y 从小到大排序 
  return a.x==b.x?a.y<b.y:a.x<b.x;
}
po g_x(po a,po b){//平面上两点做差 
  return (po){(b.x-a.x),(b.y-a.y)};
}
double c_a(po a,po b){//叉积 
  return a.x*b.y-a.y*b.x;
}
void g_t(){//找凸包 
  
  //下凸包 
  
  //先读入两点，初始化 
  s_s[++x_s]=1;
  s_s[++x_s]=2;
  for(int i=3;i<=n;i++){//尝试每个点 
    po u=g_x(p_p[s_s[x_s-1]],p_p[s_s[x_s]]); 
    po v=g_x(p_p[s_s[x_s]],p_p[i]);
    while(c_a(u,v)<0.0){//叉积 
      if(x_s==1)break;//就剩一个点了 
      x_s--;//将队头放弃
      
      //继续比较叉积 
      u=g_x(p_p[s_s[x_s-1]],p_p[s_s[x_s]]);
      v=g_x(p_p[s_s[x_s]],p_p[i]);
    }
    s_s[++x_s]=i;//当前点入队 
  }
  
  //上图包 
  
  
  //先读入两点  
  s_s[++x_s]=n;
  s_s[++x_s]=n-1;
  for(int i=n-2;i>=1;i--){//尝试每个点 
    po u=g_x(p_p[s_s[x_s-1]],p_p[s_s[x_s]]);
    po v=g_x(p_p[s_s[x_s]],p_p[i]);
    while(c_a(u,v)<0.0){//叉积 
      x_s--;//将队头放弃 
      
      //继续比较叉积 
      u=g_x(p_p[s_s[x_s-1]],p_p[s_s[x_s]]);
      v=g_x(p_p[s_s[x_s]],p_p[i]);
    } 
    s_s[++x_s]=i;//当前点入队 
  }
}
double g_l(po a,po b){//两个点的距离 
  return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
const int m_a=1e9+10;
double a_s;
long long a_a[o_o],x_a;//判重后数组 
map<double,bool>m_p;//判重 
int main(){
  n=r_r(); 
  for(int i=1;i<=n;i++)//读入所有点的信息 
    scanf("%lf %lf",&p_p[i].x,&p_p[i].y);
  sort(p_p+1,p_p+1+n,cmp);//排序 
  g_t();//找凸包 
  for(int i=1;i<=x_s;i++){//判重 
    if(m_p[1ll*p_p[s_s[i]].x*m_a+p_p[s_s[i]].y])continue;//出现过 
    a_a[++x_a]=s_s[i];
    m_p[p_p[s_s[i]].x*m_a+p_p[s_s[i]].y]=1;//标记 
  }
  a_a[++x_a]=a_a[1];//收尾相接 
  double a_s=0.0;//初始化结果 
  for(int i=1;i<x_a;i++)a_s+=g_l(p_p[a_a[i]],p_p[a_a[i+1]]);//计算长度 
  printf("%.2lf",a_s);//输出结果 
  return 0;
}

旋转卡壳

题目让我们处理的是凸包的直径，其中一种思路是将凸包边上的所有的点处理出来后，暴力枚举这些点每两个点之间的距离，找出最大值。

下面的代码中是第二种找凸包的方式（上面的是一半一半找，下面的是通过排序直接判一遍即可。）

P1452【模板】旋转卡壳

代码（排序处理凸包）

#include<iostream>
#include<cstdlib>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<queue>
#include<vector>
#include<bitset>
#include<stack>
using namespace std;
long long r_r(){//快读 
  int f=1,x=0;
  char c=getchar();
  while(!isdigit(c)){
    if(c=='-')f=-1;
    c=getchar();
  }
  while(isdigit(c)){
    x=(x<<1)+(x<<3)+(c^48);
    c=getchar();
  }
  return x*f;
}
const int m_a=0x3f3f3f3f;//最大值 
const int o_o=1e5+10;
struct po{//维护每个节点 
  int x;
  int y;
}p_p[o_o],s_s[o_o],t_p;
int n,t_t;
int c_a(po a,po b,po c,po d){//叉积 
  return (b.x-a.x)*(d.y-c.y)-(b.y-a.y)*(d.x-c.x);
}
long long g_l(po a,po b){//两点距离平方 
  return (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y);
}
bool cmp(po a,po b){
  int g_s=c_a(p_p[0],a,p_p[0],b);//叉积 
  if(g_s>0)return 1;//b 在 1 号节点和 a 的顺时针位置，交换位置（将 a 替换掉） 
  else if(!g_s)return g_l(p_p[0],a)<g_l(p_p[0],b);//在一条线上，距离近的在前 
  return 0;//不交换位置 
}
void b_t(){
  
  //初始化 
  t_p.x=m_a;
  t_p.y=m_a;
  int a_i=0;
  
  //记录最右边最上边的点 
  for(int i=0;i<n;i++)
    if(t_p.y>p_p[i].y||t_p.y==p_p[i].y&&t_p.x>p_p[i].x){
      t_p=p_p[i];
      a_i=i;//记录编号 
    }
  swap(p_p[0],p_p[a_i]);//将当前点变成第一个点 
  sort(p_p+1,p_p+n,cmp);//所有节点排序（不包括第一个节点） 
  s_s[0]=p_p[0];//记录第一个点 
  for(int i=1;i<n;i++){
    while(c_a(s_s[t_t-1],s_s[t_t],s_s[t_t],p_p[i])<=0&&t_t)t_t--;
    //找凸点 
    s_s[++t_t]=p_p[i];//记录 
  }
}
long long g_a(){
  long long a_s=0;
  s_s[++t_t]=p_p[0];//记录第一个点 
  for(int i=0;i<t_t;i++)//枚举所有点 
    for(int j=i+1;j<t_t;j++)//枚举所有点 
      a_s=max(a_s,g_l(s_s[i],s_s[j]));//查找最大值 
  return a_s;
}
int main(){
  n=r_r();
  for(int i=0;i<n;i++)//读取每个节点坐标 
    p_p[i].x=r_r(),p_p[i].y=r_r();
  b_t();//处理凸包 
  printf("%lld",g_a());//处理结果 
  return 0;
}

代码（一半一半找凸包法）

#include<iostream>
#include<cstdlib>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<queue>
#include<vector>
#include<bitset>
#include<stack>
#include<map>
using namespace std;
long long r_r(){
  long long k=0,f=1;
  char c=getchar();
  while(!isdigit(c)){
    if(c=='-')f=-1;
    c=getchar();
  }
  while(isdigit(c)){
    k=(k<<1)+(k<<3)+(c^48);
    c=getchar(); 
  }
  return k*f;
}
const int o_o=1e6+10;
long long n;
struct po{
  long long x;
  long long y;
}p_p[o_o];
long long s_s[o_o],x_s;
bool cmp(po a,po b){
  return a.x==b.x?a.y<b.y:a.x<b.x;
}
po g_x(po a,po b){
  return(po){(b.x-a.x),(b.y-a.y)};
}
long long c_a(po a,po b){
  return a.x*b.y-a.y*b.x;
}
void g_t(){
  s_s[++x_s]=1;
  s_s[++x_s]=2;
  for(int i=3;i<=n;i++){
    po u=g_x(p_p[s_s[x_s-1]],p_p[s_s[x_s]]); 
    po v=g_x(p_p[s_s[x_s]],p_p[i]);
    while(c_a(u,v)<0.0){
      if(x_s==1)break;
      x_s--;
      u=g_x(p_p[s_s[x_s-1]],p_p[s_s[x_s]]);
      v=g_x(p_p[s_s[x_s]],p_p[i]);
    }
    s_s[++x_s]=i;
  }
  s_s[++x_s]=n;
  s_s[++x_s]=n-1;
  for(int i=n-2;i>=1;i--){
    po u=g_x(p_p[s_s[x_s-1]],p_p[s_s[x_s]]);
    po v=g_x(p_p[s_s[x_s]],p_p[i]);
    while(c_a(u,v)<0.0){
      x_s--;
      u=g_x(p_p[s_s[x_s-1]],p_p[s_s[x_s]]);
      v=g_x(p_p[s_s[x_s]],p_p[i]);
    } 
    s_s[++x_s]=i;
  }
}
double g_l(po a,po b){
  return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
long long g_2(po a,po b){
  return (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y);
}
const int m_a=1e9+10;
long long a_s;
long long a_a[o_o],x_a;
map<long long,bool>m_p;
void f_i(){
  s_s[++x_a]=s_s[1];
  for(int i=1;i<=x_a;i++)
    for(int j=i+1;j<=x_a;j++)a_s=max(a_s,g_2(p_p[a_a[i]],p_p[a_a[j]]));
}
int main(){
  n=r_r(); 
  for(int i=1;i<=n;i++)
    p_p[i].x=r_r(),p_p[i].y=r_r();
  sort(p_p+1,p_p+1+n,cmp);
  g_t();
  for(int i=1;i<=x_s;i++){//判重 
    if(m_p[1ll*p_p[s_s[i]].x*m_a+p_p[s_s[i]].y])continue;
    a_a[++x_a]=s_s[i];
    m_p[1ll*p_p[s_s[i]].x*m_a+p_p[s_s[i]].y]=1;
  }
  f_i();
  printf("%ld",a_s);
  return 0;
}

但是，由于调用的 map 来判重，它的内部是一棵树，所以会有不稳定的复杂度，更推荐第一种解法。

凸包模板题也可以用第一种解法，这里不再赘述。

三维凸包

P4724 【模板】三维凸包

• 加减运算：

三维对应的值加减。

• 模长：

$$|\vec{a}|=\sqrt{x^2+y^2+z^2}$$ $$|\vec{AB}|=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2+(z_B-z_A)^2}$$

• 点积：

三维对应值相乘的和。

$$A\cdot B=(x_A\times x_B+y_A\times y_B+z_A\times z_B)$$

判断位置：

• $< 0$ 方向基本（不是完全，还有一维）相反，夹角在 $(90,180)$ 之间 。

• $> 0$ 方向基本相同，夹角在 $(0,90)$ 之间 。

• $= 0$ 正交（垂直）。

在代码中，我们用四数判断是否为“凸点”时，表达式：

（目前已有 $a,b,c$，新点是 $x$）

$$(x-a)\cdot((b-a)\times (c-a))$$

和 $0$ 的大小关系。（注意点差乘的区别。）

• 叉积：

$$A\times B=\{ y_A\times z_B-z_A\times y_B,z_A\times x_B-x_A\times z_B,x_A\times y_B-y_A\times x_B\}$$

• 计算三角形面积（上面有）：

$$S_{\Delta ABC}= \frac{1}{2}\lvert \vec{AB}\times \vec{AC}\rvert$$

• 扰动：

我们用的是三角形计算法，但是难免会出现多点共面，同时题目要求的精度又非常低。

这时我们可以让每个点的位置移动一点点（真的一点点，精度允许范围内！），虽然我们的精度没变，但是几点面的定义确实严格的，不能又丝毫偏差。

这样就可用三角形求面积法了。

代码

#include<iostream>
#include<cstdlib>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<queue>
#include<vector>
#include<bitset>
#include<stack>
#include<map>
using namespace std;
long long r_r(){//快读 
  long long k=0,f=1;
  char c=getchar();
  while(!isdigit(c)){
    if(c=='-')f=-1;
    c=getchar();
  }
  while(isdigit(c)){
    k=(k<<1)+(k<<3)+(c^48);
    c=getchar(); 
  }
  return k*f;
}
const long long o_o=2e4+10;
const double m_i=1e-9;//极小值 
struct p_1{//记录点 
  double x,y,z;
  void r_d(){//点的坐标 
    scanf("%lf %lf %lf",&x,&y,&z);
  }
  p_1 operator +(const p_1&n)const{//加法 
    return {x+n.x,y+n.y,z+n.z};
  }
  p_1 operator -(const p_1&n)const{//减法 
    return {x-n.x,y-n.y,z-n.z};
  }
  p_1 operator *(const p_1&n)const{//叉乘 
    return {y*n.z-z*n.y,z*n.x-x*n.z,x*n.y-y*n.x};
  }
  double operator ^(const p_1&n)const{//点积 
    double a_s=x*n.x+y*n.y+z*n.z;
    return a_s;
  }
}p_p[o_o];//存点的基本信息 
long long n,m,x_n;
double l_x(p_1 k){//模长 
  return sqrt(k^k);
}
struct p_2{//记录面 
  long long x,y,z;//这里不是坐标，是三个点的序号
  //或者说，当前面由上面三个点确定的 
   
  bool c_a(p_1 a_s){//判断位置 
    //右手，食指指向第一个向量的方向，中指指向第二个向量的方向，大拇指为结果方向
    //用来判断点的位置 
     
    //<0 方向基本（不是完全，还有一维）相反，夹角在 90 ~ 180 之间 
    //>0 方向基本相同，夹角在 0 ~ 90 之间 
    //=0 正交 
    return ((a_s-p_p[x])^((p_p[y]-p_p[x])*(p_p[z]-p_p[x])))>0?1:0;
  }
};
void g_i(double&x){//随机小数（数要足够小，这样不会影响结果） 
  x=x+((double)rand()/(double)RAND_MAX-0.5)*m_i*10;
}
void r_d(){//读入 
  x_n=r_r();//点数 
  for(int i=1;i<=x_n;i++){
    p_1 p;
    p.r_d();//读入点的基本信息 
    bool b_p=0;
    for(int j=1;j<=n;j++)
      //这个点和另一个点无限接近，那么这个点就不要了（精度可以承受） 
      if(fabs(p.x-p_p[j].x)<=m_i&&fabs(p.y-p_p[j].y)<=m_i&&fabs(p.z-p_p[j].z)<=m_i){
        b_p=1;//标记，不要了 
        break;
      }
    if(!b_p)p_p[++n]=p;//读入当前点的信息 
  }
  for(int i=1;i<=n;i++){//扰动 
    g_i(p_p[i].x);
    g_i(p_p[i].y);
    g_i(p_p[i].z);
  }
}
bool b_b[o_o][o_o];
double g_a(){
  vector<p_2>x_x;
  
  //将前三个点先入队 
  x_x.push_back((p_2){1,2,3});
  x_x.push_back((p_2){3,2,1});
  for(long long i=4;i<=n;i++){//从第四个点开始处理 
    vector<p_2>k_k;
    for(long long j=0;j<x_x.size();j++){
      bool b_p=x_x[j].c_a(p_p[i]);//判断位置 
      if(!b_p)k_k.push_back(x_x[j]);//是凸点，入队 
      
      //标记 
      b_b[x_x[j].x][x_x[j].y]=b_p;
      b_b[x_x[j].y][x_x[j].z]=b_p;
      b_b[x_x[j].z][x_x[j].x]=b_p;
    }
    
    //没有处理过这两个点的入队（x,y 处理和 y,x 处理是一个意思，所以要判重） 
    for(long long j=0;j<x_x.size();j++){
      //两个点和当前点的入队（三点成面，最后统计面积） 
      if(b_b[x_x[j].x][x_x[j].y]!=b_b[x_x[j].y][x_x[j].x]&&b_b[x_x[j].x][x_x[j].y])
        k_k.push_back((p_2){x_x[j].x,x_x[j].y,i});
      if(b_b[x_x[j].y][x_x[j].z]!=b_b[x_x[j].z][x_x[j].y]&&b_b[x_x[j].y][x_x[j].z])
        k_k.push_back((p_2){x_x[j].y,x_x[j].z,i});
      if(b_b[x_x[j].z][x_x[j].x]!=b_b[x_x[j].x][x_x[j].z]&&b_b[x_x[j].z][x_x[j].x])
        k_k.push_back((p_2){x_x[j].z,x_x[j].x,i});
    }
    x_x=k_k;//更新 
  }
  double a_s=0;
  for(long long i=0;i<x_x.size();i++)//统计答案（向量求三角形面积） 
    a_s+=l_x((p_p[x_x[i].y]-p_p[x_x[i].x])*(p_p[x_x[i].z]-p_p[x_x[i].x]))/2;
  return a_s;
}
int main(){
  r_d();//读入 
  printf("%.3lf",g_a());//输出 
  return 0;
 } 

半平面交

P4196 【模板】半平面交

每次处理图形，将新图形的边和原图形每条边比较，更新找到最大图形（有些时候两边相交要维护交点）。

最后存的是所有图形的外轮廓的节点（也就是覆盖的面积的多边形的所有顶点），最后通过三角形面积法计算面积即可。

代码

#include<iostream>
#include<cstdlib>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<queue>
#include<vector>
#include<bitset>
#include<stack>
#include<map>
using namespace std;
long long r_r(){//快读 
  long long k=0,f=1;
  char c=getchar();
  while(!isdigit(c)){
    if(c=='-')f=-1;
    c=getchar();
  }
  while(isdigit(c)){
    k=(k<<1)+(k<<3)+(c^48);
    c=getchar(); 
  }
  return k*f;
}
const int o_o=1e3+10;
struct po{
  double x,y;
  po operator -(const po n){//减法 
    return (po){x-n.x,y-n.y};
  }
  po operator +(const po n){//加法 
    return (po){x+n.x,y+n.y};
  }
  po operator *(double t){//乘法（缩放） 
    return (po){x*t,y*t};
  }
  double c_a(po n){//叉积 
    return x*n.y-y*n.x;
  }
}a_i[o_o],b_i[o_o],c_i[o_o];
int n,m,x_c,x_p;
void a_d(po a_1,po a_2,po b_1,po b_2){
  po k_1=a_2-a_1;
  po k_2=b_2-b_1;
  po k_3=b_1-a_1;
  double t=k_2.c_a(k_3)/k_2.c_a(k_1);//计算斜率 
  c_i[++x_c]=a_1+k_1*t;//记录交点   
}
void f_i(po a,po b){//维护最大覆盖图形 
  x_c=0;
  a_i[x_p+1]=a_i[1];
  for(int i=1;i<=x_p;i++)
    if((a-a_i[i]).c_a(b-a_i[i])>=0){//在顺时针方向或同向 
      c_i[++x_c]=a_i[i];//记录节点 
      if((a-a_i[i+1]).c_a(b-a_i[i+1])<0)//逆时针方向 
        a_d(a_i[i],a_i[i+1],a,b);//记录交点 
    }else if((a-a_i[i+1]).c_a(b-a_i[i+1])>=0)//在下一个点的顺时针方向 
      a_d(a_i[i],a_i[i+1],a,b);//记录交点 
  for(int i=1;i<=x_c;i++)a_i[i]=c_i[i];//更新节点 
  x_p=x_c;//更新节点数 
}
double c_s(){
  //所有剩下的点，根据三角形求面积 
  double a_s=0;
  for(int i=2;i<x_p;i++)a_s+=(a_i[i]-a_i[1]).c_a(a_i[i+1]-a_i[1]);
  return a_s/2;
}
int main(){
  n=r_r(),m=r_r();
  x_p=m;//记录图形的节点数量 
  n--;//单独处理第一个图形 
  for(int i=1;i<=m;i++){//记录当前图形所有的点 
    a_i[i].x=r_r();
    a_i[i].y=r_r();
  }
  while(n--){//处理剩下的图形 
    m=r_r();//图形点的数量 
    
    //读入节点 
    b_i[1].x=r_r();
    b_i[1].y=r_r();
    b_i[m+1]=b_i[1];
    for(int i=2;i<=m;i++){
      b_i[i].x=r_r();
      b_i[i].y=r_r();
    }
    
    //处理新图形所有相邻节点 
    for(int i=1;i<=m;i++)f_i(b_i[i],b_i[i+1]);
  }
  printf("%.3f\n",c_s());//统计结果 
  return 0;
}

代码（极角排序）

• 极角排序

$\arctan$ 函数图像

（如果不能自动跳，点击文章目录的“函数作图”标签，往下略翻，即可看到。）

不难发现，它是单调的，可以用来排序。

同样可以使用叉积来实现极角排序。

这里我们同 $\arctan$ 函数来处理。

$$\tan x\times \arctan x=1$$

• 边处理

不难发现，凸多边形和凸多边形交的“特出地方”会出现“凹陷”的地方，我们就是将所有“凹陷”里的交点，统计出来。

同时用双端队列，将没有交点的边（“无关人士”）“弹”走，交点仍然要通过斜率计算（和上面一样），记录点。

最后，计算面积的时候仍然用三角形面积法。

#include<iostream>
#include<cstdlib>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<queue>
#include<vector>
#include<bitset>
#include<stack>
#include<map>
using namespace std;
long long r_r(){//快读 
  long long k=0,f=1;
  char c=getchar();
  while(!isdigit(c)){
    if(c=='-')f=-1;
    c=getchar();
  }
  while(isdigit(c)){
    k=(k<<1)+(k<<3)+(c^48);
    c=getchar(); 
  }
  return k*f;
}
const int o_o=1e3+10;
const double m_i=1e-10;
int n,m,s_m;
struct po{
  double x,y;
  po operator+(const po&a)const{//加法 
    return {x+a.x,y+a.y};
  }
  po operator-(const po&a)const{//减法 
    return {x-a.x,y-a.y};
  }
  po operator*(const double&a)const{//乘法 
    return {x*a,y*a};
  }
  po operator/(const double&a)const{//除法 
    return {x/a,y/a};
  }
}p_p[1100],x_x[1100];
double c_1(po x,po y){//叉积 
  return x.x*y.y-x.y*y.x;
}
struct b_n{
  po x,y;//两个端点 
  double k;//方便极角排序 
  b_n g_k(po a,po b){
    x=a;
    y=b;
    k=atan2(y.y,y.x);
  }
  bool operator<(const b_n&a)const{//排序方式 
    return k<a.k;
  }
}k_k[1100],s_s[1100];
int h_i,t_i;
po g_t(b_n x,b_n y){//处理交点 
  po k_k=x.x-y.x;
  double t=c_1(y.y,k_k)/c_1(x.y,y.y);
  return x.x+x.y*t; 
}
void f_i(){
  //初始化 
  h_i=t_i=1;
  s_s[h_i]=k_k[1];
  
  for(int i=2;i<=s_m;i++){
    
    //交点在逆时针方向 
    while(h_i<t_i&&c_1(k_k[i].y,x_x[t_i-1]-k_k[i].x)<=m_i)--t_i;
    while(h_i<t_i&&c_1(k_k[i].y,x_x[h_i]-k_k[i].x)<=m_i)++h_i;
    
    s_s[++t_i]=k_k[i];//加上当前的边 
    if(fabs(c_1(s_s[t_i].y,s_s[t_i-1].y))<=m_i){//平行 
      t_i--;
      
      //记录平行中左边的 
      if(c_1(s_s[t_i].y,k_k[i].x-s_s[t_i].x)>m_i)s_s[t_i]=k_k[i];
    }
    if(h_i<t_i)x_x[t_i-1]=g_t(s_s[t_i-1],s_s[t_i]);//加入交点
  }
  while(h_i<t_i&&c_1(s_s[h_i].y,x_x[t_i-1]-s_s[h_i].x)<=m_i)--t_i;
  if(t_i-h_i<=1)return;//没边了 
  x_x[t_i]=g_t(s_s[h_i],s_s[t_i]);//记录 
}
void g_a(){//三角形面积法 
  double a_s=0;
  for(int i=h_i;i<=t_i;i++){
    int k=i+1;
    if(i==t_i)k=h_i;
    a_s+=c_1(x_x[i],x_x[k]);
  }
  printf("%.3lf",a_s/2);
}
int main(){
  int n=r_r();
  for(int i=1;i<=n;i++){
    m=r_r();
    for(int j=1;j<=m;j++)scanf("%lf%lf",&p_p[j].x,&p_p[j].y);//存点 
    for(int j=1;j<=m;j++){//加边 
      ++s_m;
      int k=j+1;
      if(j==m)k=1;
      k_k[s_m].g_k(p_p[j],p_p[k]-p_p[j]);
    }
  }
  sort(k_k+1,k_k+s_m+1);//极角排序 
  f_i();//处理边 
  g_a();//统计结果 
  return 0;
}